Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.2 - Ex. 27
27. Use métodos vetoriais para provar que sempre é retângulo qualquer triângulo inscrito num círculo de tal modo que um de seus lados seja um diâmetro. [Sugestão: expresse os vetores e da figura dada em termos de e
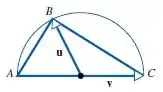
Passo 1
Bem... vamos usar a sugestão, ne...
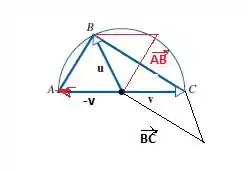
Então pelo que sabemos da soma de vetores (usando o maravilhoooooso desenho que fiz dá pra ver melhor
Usando o paralelogramo da parte em preto:
Usando agora o vermelho:
Passo 2
Pra ser um triângulo retângulo, o ângulo entre os dois vetores tem que ser 90°,ne...
Ou seja, o produto interno entre os dois vetores tem que ser zero:
Como , então:
Lembrando que é a norma de , ou seja, o tamanho do vetor...
Como eles têm o mesmo tamanho (que é o raio), então:
Como queríamos demonstrar.
Resposta
Demonstração.
Exercícios de Livros Relacionados
Sejam SeS 0 subconjuntos de um espaço vetorial com produto interno V . Mostre que S 0 ⫅ S implica que S ⊥ ⫅ S 0 ⊥ .
Seja w um subespaço de um espaço vetorial com produto interno V gerado pelos vetores V 1 , … , V k . Mostre que V ∈ w ⊥ se, e somente se, V é ortogonal a V i , para i = 1 , … , k .
Seguindo os mesmos passos do exercício anterior mostre a seguinte fórmula de recorrência para os polinômios de Legendre: p n + 1t = 2 n + 1 n + 1 t p n t - n n + 1p n - 1 ( t )
Seja V = C 0 [ - 1,1 ] o conjunto das funções contínuas do intervalo [ - 1,1 ] em R com o produto interno definido porf , g =∫ - 1 1 f t g t d t Prove a seguinte fórmula de recorrência para os polinôm
(Desigualdade de Bessel) Seja { U 1 , … , U m } uma base ortonormal de um subespaço w de um espaço vetorial com produto interno V . Mostre que V 2 ≥ ∑ j = 1 m |V , U j 2 , ∀ V ∈ V .