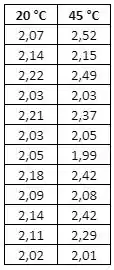
Acredita-se que a resistência à tensão da borracha siliconizada seja uma função da temperatura de cura. Um estudo foi realizado, no qual amostras de 12 espécimes de borracha foram preparadas usando temperaturas de cura de 20 °C e 45 °C. A tabela abaixo mostra os valores de resistência à tensão, em megapascals, para cada temperatura:

Usando o MATLAB, responda às seguintes questões:

1. Qual a média de resistência à tensão de cada amostra?
2. Qual é o desvio padrão de resistência à tensão para cada temperatura? O aumento de temperatura parece influenciar a variabilidade de resistência à tensão?
3. Em estatística, a amplitude é a diferença entre o maior e o menor valor de um conjunto de dados. Para cada temperatura, qual é a amplitude de resistência à tensão?

A primeira coisa que vamos fazer é entrar no Command Window dois vetores, um para cada coluna da tabela. Vamos fazer isso porque, pra usar os comandos de média, desvio padrão, mínimo e máximo, precisamos dos dados todos juntinhos num vetor (um pra cada temperatura).

T_20 = [2.07 2.14 2.22 2.03 2.21 2.03 2.05 2.18 2.09 2.14 2.11 2.02];

T_45 = [2.52 2.15 2.49 2.03 2.37 2.05 1.99 2.42 2.08 2.42 2.29 2.01];

O vetor T_20 contém os valores de resistência à tensão da primeira coluna da tabela, referente a 20 °C. Já o vetor T_45 contém os valores da segunda coluna da tabela, referente a 45 °C. Por enquanto, temos isso aqui no MATLAB:

Dica: coloquei o ; no final de cada comando para o MATLAB não imprimir o vetor logo depois de eu entrar com ele. Dessa forma, nosso Command Window fica menos poluído.

Agora vamos calcular a média de cada vetor. Para isso, vamos usar a função mean() duas vezes, uma em cada vetor:

media_20 = mean(T_20)

media_45 = mean(T_45)

A primeira linha de código acima vai retornar a média dos valores do vetor T_20 e armazenar a média em uma variável chamada media_20.

A segunda linha de código acima vai retornar a média dos valores do vetor T_45 e armazenar a média em uma variável chamada media_45. Note que ambas as linhas não têm o ; no final. Logo, o MATLAB vai imprimir pra gente o resultado no Command Window.

No MATLAB, ficou assim:

Portanto, a média de resistência à tensão para amostra submetida a uma temperatura de cura de 20 °C é 2,1075 Mpa.

Já a média para a amostra submetida a uma temperatura de cura de 45 °C é 2,2350 MPa. Dessa forma, a letra a está resolvida e podemos partir para a letra b.

Na letra b, devemos calcular o desvio padrão de cada amostra. Para isso, vamos usar a função std(). No Command Window, entre as duas linhas de código:

d_pad_20 = std(T_20)

d_pad_45 = std(T_45)

Na primeira linha de código, pedimos ao MATLAB que calcule o desvio padrão dos valores do vetor T_20 e armazene o desvio padrão em uma variável chamada d_pad_20.

Na segunda linha de código, pedimos ao MATLAB que calcule o desvio padrão dos valores do vetor T_45 e armazene o desvio padrão em uma variável chamada d_pad_45. O Command Window do MATLAB nos imprime essas respostas:

Portanto, o desvio padrão da amostra de 20 °C é de 0,0709 MPa e o desvio padrão da amostra de 45°C é de 0,2032 MPa.

A letra b da questão pede para refletirmos se o aumento da temperatura tem algum impacto na variabilidade da amostra. Podemos fazer essa reflexão a partir dos valores de desvio padrão que encontramos, já que o desvio padrão serve para avaliar a variabilidade de uma amostra. Quanto maior o desvio padrão, maior a variabilidade.

Repare que d_pad_20 é menor que d_pad_45, indicando que a amostra com temperatura de cura de 20 °C tem menor variabilidade quando comparada com a amostra com temperatura de cura de 45 °C. Logo, há indícios de que o aumento da temperatura aumenta a variabilidade de resistência à tensão.

Finalmente, vamos resolver a letra c. Para calcularmos a amplitude das amostras, devemos antes encontrar os valores máximo e mínimo de resistência à tensão de cada amostra. Para isso, vamos usar a função max(), para encontrar a maior resistência de cada coluna da tabela, e a função min(), para encontrar a menor. Vamos entrar as quatro linhas de código:

min_20 = min(T_20)

max_20 = max(T_20)

min_45 = min(T_45)

max_45 = max(T_45)

Na primeira linha de código, pedimos ao MATLAB que nos dê o menor valor do vetor T_20 e que o menor valor seja armazenado na variável min_20. Já na segunda linha de código, pedimos ao MATLAB que nos dê o maior valor do vetor T_20 e que o maior valor seja armazenado na variável max_20.

As linhas 3 e 4 fazem a mesma coisa, mas para o vetor T_45. Bora ver como fica no MATLAB:

Para calcular a amplitude de cada amostra, fazemos a diferença entre o valor máximo e mínimo de cada temperatura, por meio das duas linhas de código:

amp_20 = max_20 - min_20

amp_45 = max_45 - min_45

Na primeira linha, calculamos a amplitude para a amostra de 20 °C e armazenamos o resultado na variável amp_20.

Na segunda linha, calculamos a amplitude para a amostra de 45 °C e armazenamos o resultado na variável amp_45. Vamos ver a resposta que o MATLAB nos deu:

Temos que a amplitude de resistência à tensão para a amostra de 20 °C é de 0,2 MPa e que a amplitude para 45 °C é de 0,53 MPa.