Na definição de autovalores e autovetores, temos que, dada uma matriz quadrada A:
onde V é uma matriz cujas colunas correspondem aos autovetores e D é uma matriz diagonal, em que os elementos da diagonal principal são os autovalores da matriz A.
Usando o MATLAB, dada a matriz:
- Encontre os autovalores e os autovetores de A;
- Verifique a igualdade .
Passo 1
A questão pede que apliquemos diretamente a função eig() do MATLAB na matriz A (letra a da questão) e, em seguida, verifiquemos a igualdade (letra b). Usando diretamente as saídas da função eig(), podemos resolver a letra b, já que a função eig()nos retorna as matrizes V e D exatamente no formato descrito no enunciado.
Passo 2
Vamos começar com a letra a, que nos pede para encontrar os autovalores e os autovetores da matriz A. Primeiramente, temos que entrar com a matriz A no MATLAB, no Command Window, com a seguinte linha de código:
A = [6 7 1 8; 5 3 1 7; 3 6 5 7; 0 7 4 0]
No Command Window do MATLAB, fica assim:

Em seguida, aplicamos diretamente a função eig() para encontrar os autovalores e os autovetores de A, entrando com o seguinte comando do Command Window:
[V,D] = eig(A)
Com esse comando, pedimos à função eig() que nos informe os autovalores e os autovetores de A e ela nos retorna duas matrizes: V e D. vamos ver como isso fica no MATLAB:
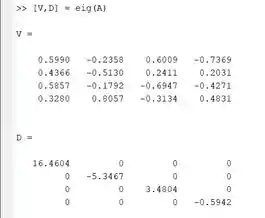
A matriz V apresenta os autovetores de A: cada coluna de V é um autovetor de A. Já a matriz D é uma matriz diagonal que nos apresenta os autovalores de A. Cada elemento da diagonal principal de D é um autovalor.
Portanto, os autovetores da matriz A são:
E os autovalores são:
Passo 3
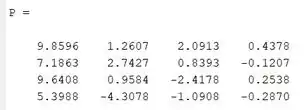
Concluindo a letra a da questão, temos as matrizes V e D para verificar a igualdade . Primeiramente, fazemos o produto e em seguida, o produto , e comparamos os resultados. Vamos ver como fica no Command Window do MATLAB:
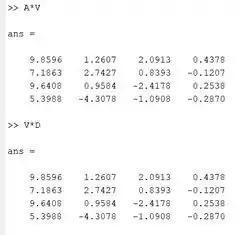
Veja que os resultados são idênticos. Logo, .
Resposta
- Os autovetores da matriz A são:
- Utilizando [V,D] = eig(A) , encontramos as matrizes V e D no formato adequado para verificar a igualdade . O produto e o produto resultam na mesma matriz, que chamarei de P, apresentada abaixo:
E os autovalores são: