Considere o corpo rígido abaixo, que possui três graus de liberdade rotacionais:

A matriz de momentos de inércia do corpo rígido tem a forma:

onde os momentos de inércia, em kgm², são definidos de acordo com o sistema de coordenadas .

É possível determinar um novo sistema de coordenadas, com eixos ortogonais, de forma que a matriz seja diagonal. Esses eixos ortogonais do novo sistema de coordenadas são chamados de eixos principais, e os momentos de inércia associados a eles são chamados de momentos de inércia principais. Os momentos de inércia principais são dados pelos autovalores de e os eixos principais, pelos autovetores de . Com o MATLAB, determine os eixos principais e os momentos de inércia principais para a matriz .

Passo 1

A questão nos mostra a matriz de momentos de inércia de um corpo rígido e nos pede para encontrarmos os eixos principais e os momentos de inércia principais a partir de . Os eixos principais são os autovetores de e os momentos de inércia principais são os autovalores de . Este exercício é resolvido usando a função eig() do MATLAB, que nos dá os autovalores e os autovetores de uma matriz.

Passo 2

Primeiramente, entramos a matriz no Command Window do MATLAB usando o código:

I_rot = [150 0 -100;0 250 0;-100 0 500]

Em seguida, usamos a função eig(), tendo I_rot como entrada, entrando com o comando:

[dir_princ,mom_princ] = eig(I_rot)

Nesse comando, pedimos ao MATLAB que encontre os autovetores e os autovalores da matriz I_rot. Os autovetores são armazenados na variável dir_princ e os autovalores, na variável mom_princ. No Command Window do MATLAB, fica assim:

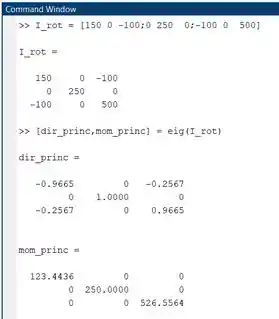
Os autovetores de I_rot são as colunas da matriz dir_princ. Logo, os eixos principais são definidos pelos vetores:

Os autovalores de I_rot são os elementos da diagonal principal da matriz mom_princ. Logo, os momentos de inércia principais são:

123,4436 kgm²

250 kgm²

526,5564 kgm²

Resposta

Os eixos principais definidos a partir de são representados pelos vetores:

Os momentos de inércia principais definidos a partir de são:

123,4436 kgm²

250 kgm²

526,5564 kgm²

Resposta