Cinco analistas obtiveram os resultados (mmol de Ca), mostrados na tabela que se segue, para a determinação de cálcio por um método volumétrico. As médias diferem significativamente em um nível de confiança de ?
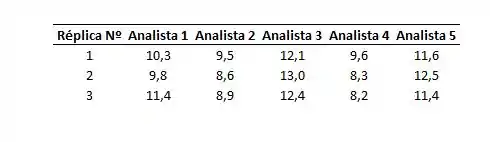
Passo 1
Nessa questão temos cinco séries de dados, e precisamos determinar se as médias populacionais entre elas são iguais, ou seja, precisamos comprovar a hipótese nula abaixo:
Para isso, vamos utilizar um método chamado ANOVA. Esse método analisa a variância de diferentes séries de dados para determinar se elas têm médias populacionais equivalentes
Passo 2
Para começar, precisamos calcular a média aamostral de cada uma das séries.
A média populacional pode ser encontrada através da fórmula abaixo:
Para o primeiro analista, essa média seria:
Para os demais grupos, essa média pode ser encontrada na tabela abaixo:
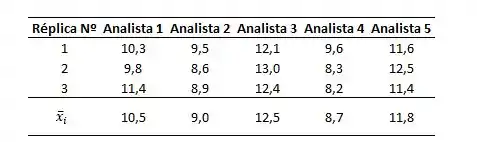
Passo 3
O próximo passo é calcular média total, ou seja, a média de todos os valores obtidos de todos analistas. Essa média pode ser calculada pela seguinte fórmula:
Passo 4
Agora vamos calular o SQF, isto é, a soma dos quadrados entre os grupos. Basicamente precisamos somar os quadrados dos erros da média de cada grupo com a média geral. Só seguir essa fórmula aqui:
A tabela abaixo mostra cada quadrado de fator:
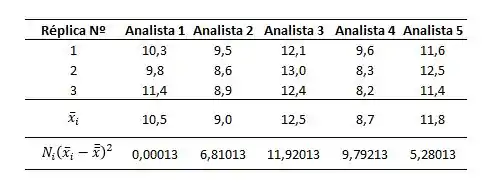
A soma dos quadrados dos fatores será portanto:
Passo 5
O próximo passo é calcilar a soma dos quadrados dos erros, ou seja, a soma dos quadrados dos erros dentro de cada grupo:
Vamos fazer isso com o auxílio da tabela também:
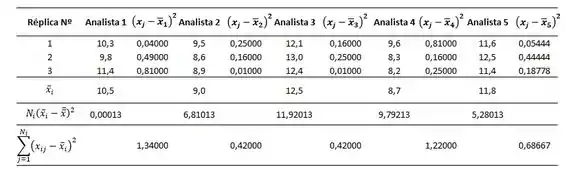
A soma dos quadrados dos erros, será portanto:
Passo 6
O próximo passo é calcular a média dos erro dividindo-os pelo seu grau de liberdade:
Onde é o número total de dados, e é o número de grupos. Portanto:
Passo 7
Estamos acabando finalmente, agora só resta calcular o valor de F e comparar com o F tabelado. Vamos usar a seguinte fórmula para achar :
Vamos então consultar a tabela abaixo para encontrar p valor de e poder comparar:
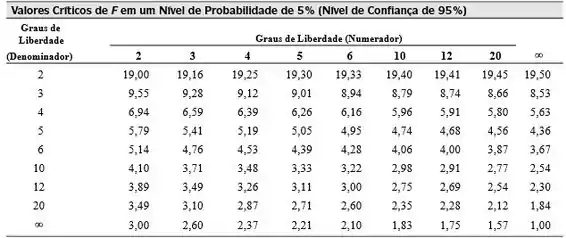
O grau de liberdade do numerador (MQF) é 4, e do denominador (SQF) é 10. Portanto, teremos:
Portanto, o que calculamos é maior que o , isso significa que precisamos rejeitar a hipótese nula, e portanto, existe diferença significativa entre as médias populacionais dos analistas.
Resposta
Existe diferença significativa entre as médias populacionais.