Três métodos analíticos diferentes são comparados em relação à determinação de Ca.Estamos interessados em saber se os métodos diferem entre si. Os resultados, expressos em ppm de Ca, representam determinações por colorimetria, titulação com EDTA e espectrometria de absorção atômica.
a) Defina as hipóteses apropriadas.
b) Determine se existem diferenças significativas entre os três métodos a níveis
de confiança de .
c) Se foi detectada a diferença a um nívelde confiança de 95%, determine quais métodos diferem dos outros
Passo 1
Nessa questão, a mesma análise foi feita através de três métodos quantitativos diferentes. Precisamos então determinar se as médias populacionais encontradas pelos diferentes métodos são equivalentes. Sendo assim, nossa hipótese nula será que todas as médias populacionais são iguais.
A hipótese alternativa, por sua vez, é que pelo menos duas das médias populacionais são diferentes entre si.
Passo 2
Vamos agora então testar nossa hipótese nula. Para fazer isso, devemos primeiro calcular as médias amostrais encontradas.
A média populacional pode ser encontrada através da fórmula abaixo:
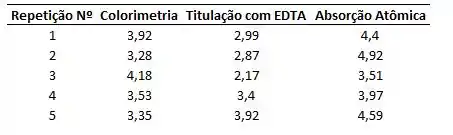
Para o primeiro analista, essa média seria:
Para os demais grupos, essa média pode ser encontrada na tabela abaixo:
Passo 3
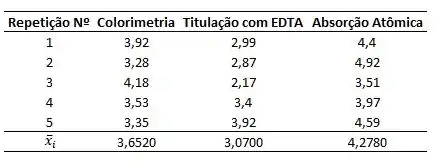
Agora, vamos calcular a média amostral de todos os valores obtidos:
Passo 4
Agora vamos calular o SQF, isto é, a soma dos quadrados entre os grupos. Basicamente precisamos somar os quadrados dos erros da média de cada grupo com a média geral. Só seguir essa fórmula aqui:
A tabela abaixo mostra cada quadrado de fator:
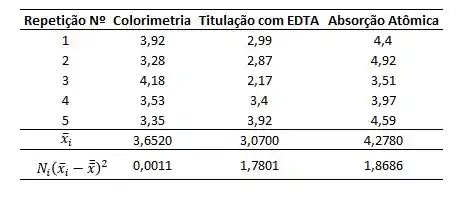
A soma dos quadrados dos fatores será portanto:
Passo 5
Além do SQF, também devemos calcular a soma dos quadrados dos erros, ou seja, a soma dos quadrados dos erros dentro de cada grupo:
Vamos fazer isso com o auxílio da tabela também:
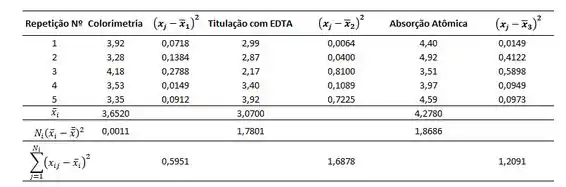
A soma dos quadrados dos erros, será portanto:
Passo 6
O próximo passo é calcular a média dos erro dividindo-os pelo seu grau de liberdade:
Onde é o número total de dados, e é o número de grupos. Portanto:
Passo 7
Estamos acabando finalmente, agora só resta calcular o valor de F e comparar com o F tabelado. Vamos usar a seguinte fórmula para achar :
Vamos então consultar a tabela abaixo para encontrar p valor de para um nível de confiança de e poder comparar:
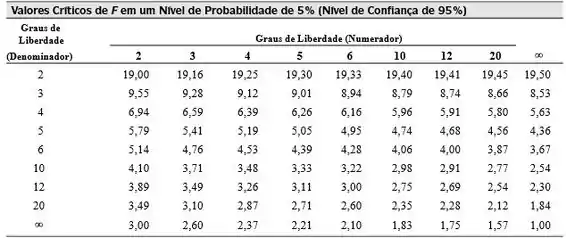
O grau de liberdade do numerador (MQF) é 2, e do denominador (SQF) é 12. Portanto, teremos:
Como , em um nível de confiança de , os resultados não são equivalentes, e a hipótese nula é falsa.
Passo 8
Para saber quais médias populacionais diferem das outras, precisamos primeiro encontrar a diferença menos significativa conforme a equação abaixo:
Onde tem nível de confiança de e grau de liberdade .
Vamos consultar a tabela abaixo para encontrar esse valor:
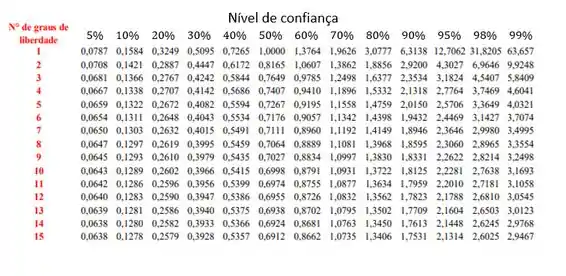
Nela, podemos ver que . Vamos então calcular a MSD:
Onde:
Passo 9
A diferença menos significativa é . Para saber quais médias diferem umas das outras, precisamos encontrar as diferenças entre elas e ver quais são maiores e quais são menores que a DMS.
Através da análise das diferenças entre as médias amostrais dos grupos, podemos ver que o grupo 1 não é significativamente diferente nem do grupo 2 nem do grupo 3. Entretanto, a diferença entre as médias amostrais dos grupos 2 e 3 é maior que a diferença menos significativa, portanto eles são significativamente diferentes.
Resposta
- falsa em 95% de nível de confiança
- Grupos 2 e 3 são diferentes