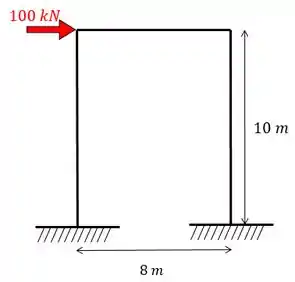
Construa o diagrama de momento fletor para o pórtico abaixo.
Passo 1
Galerinha, agora vamos resolver um problema um pouco mais complexo e também um pouco mais real, já que o queremos é de fato o momento fletor da nossa estrutura. Para resolver isso nós vamos fazer aquela separação marota entre simétrico e assimétrico.
Depois que fizermos essa separação então a gente vai calcular o momento fletor de cada estrutura e no final somar tudo!

Galera, vou deixar um aviso aqui para vocês, nos passos 3 e 4 vamos utilizar os conceitos de deformação para cálculo de estruturas hiperestáticas, existe um assunto especificamente para isso então aqui eu vou resolver de formais mais rápido para tornarmos essa resolução um pouco mais dinâmica, ok?
Vem comigo e #PartiuResolver!
Passo 2
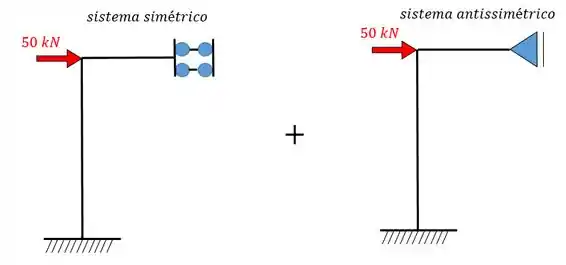
O foco nesse problema é o cálculo do momento fletor então não vou gastar muito rempo aqui discutindo sobre como fazer a separação. Vamos ter isso aqui:
Passo 3
Agora a gente vai achar o diagrama de momento fletor de cada um desses sistemas. Vamos começar com o sistema antissimétrico que é mais fácil. Para isso a gente precisa retirar o apoio de primeiro gênero e obter:
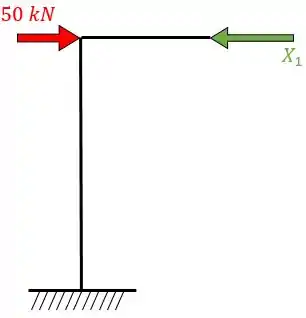
Mas para resolver a gente tem que dividir essa estrutura entre dois sistemas:
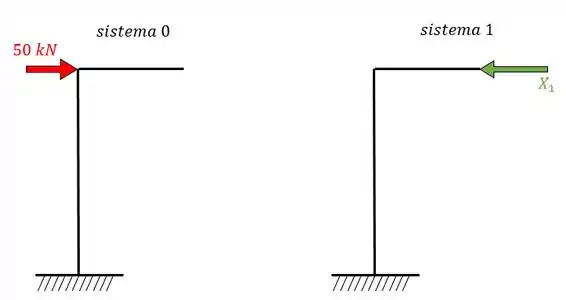
Como só existe um hiperestático então a equação dos deslocamentos é:
Agora temos de achar os deslocamentos, vamos fazer isso por meio da tabela e precisamos fazer o diagrama de momento fletor de cada sistema (considerando ). Assim, olha:
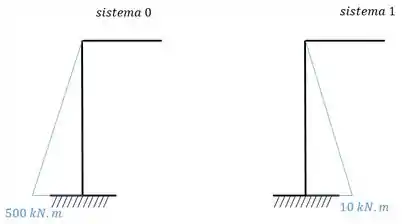
Como temos a combinação de dois triângulos então vamos ter:
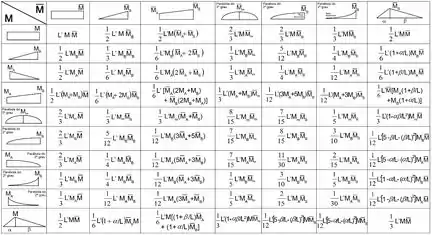
Para :
Para :
Assim podemos encontrar o nosso primeiro hiperestático:
Passo 4
Agora vamos resolver para o sistema simétrico:
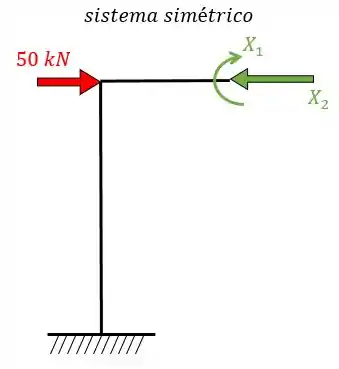
Que deve ser dividido em três sistemas:
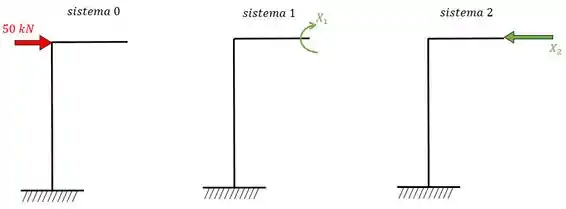
O que nos fornece o seguinte sistema de equações para a deformação:
Agora devemos fazer o diagrama de momento fletor de cada sistema:
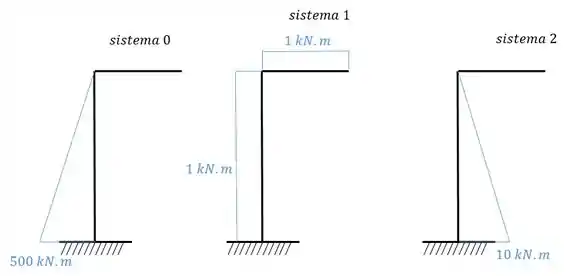
Vamos utilizar a tabela para achar as deformações:
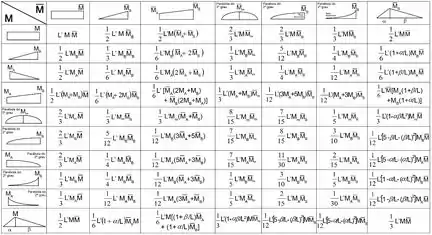
Para vamos ter:
Para vamos ter:
Para vamos ter:
Para vamos ter:
Para vamos ter que é igual a , logo:
Para vamos ter:
Agora podemos resolver nossa equação:
Substituindo
Obtendo:
Passo 5
Agora a gente pode montar as nossas estruturas da seguinte forma:
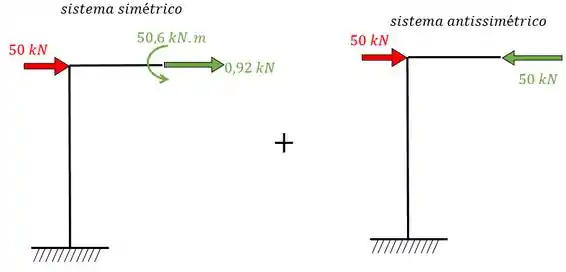
Agora temos duas estruturas isostáticas então podemos montar o diagrama de cada uma delas:

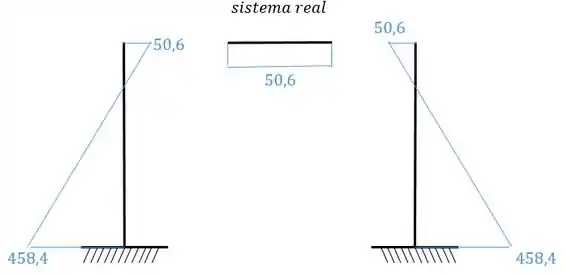
Perceba que o sistema assimétrico acabou sendo nulo! Normalmente iríamos somar ambos os sistemas e espelhar o resultado da esquerda para o lado direito, mas como o lado antissimétrico é nulo então vamos só espelhar:
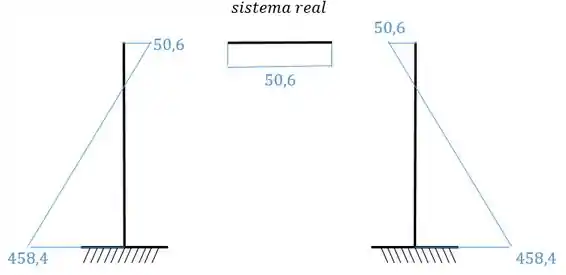
Resposta