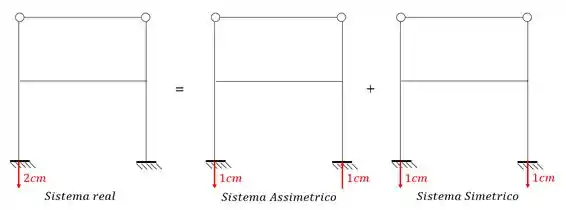
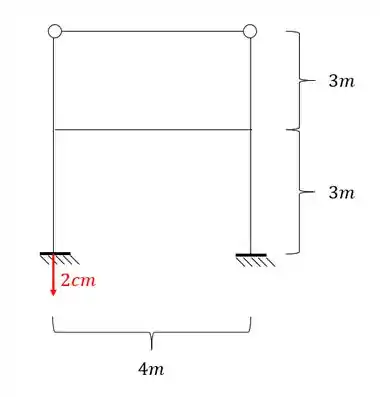
Para a estrutura abaixo, que sofre um recalque de apoio, utilize o arranjo de cargas, separando a partir do carregamento principal a estrutura com carregamento simétrico e carregamento assimétrico. Além disso, determine a estrutura mais simples a ser resolvida tanto para o caso simétrico quanto para o caso assimétrico. Determine por fim o diagrama de momentos fletores. Use :
Passo 1
O primeiro item que precisamos resolver é saber quais tipos de cargas devemos aplicar ao nosso sistema, de forma que quando unirmos o sistema simétrico ao assimétrico, dê o nosso sistema principal.
Dessa maneira sabemos que por exemplo, cada uma das cargas deverá ter a metade do seu valor, além do mais, quando unirmos cada um dos itens, a soma dessas cargas deverá dar a carga total ou zero. Dessa maneira, iremos usar exatamente esse mesmo conceito para o caso de recalque do apoio.
- Sistema principal
- Estrutura simétrica
- Estrutura Assimétrica
- Para estruturas simétricas
- Apoio de carrinho se cortar um ponto
- Apoio de engaste se cortar uma barra
- Para estruturas assimétricas
- Apoio do primeiro gênero se cortar um ponto
- Barra com metade da inércia
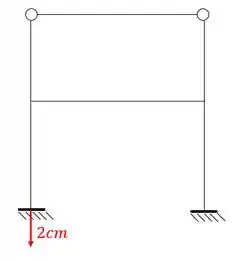
Seguindo o nosso plano, sabemos que devemos primeiro dividir esse valor pela metade, e aplica-lo na estrutura de maneira simétrica e assimétrica.
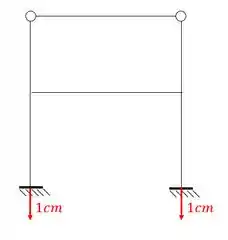
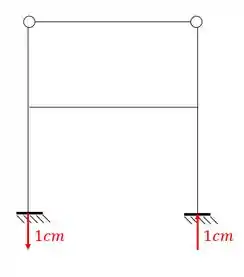
Então podemos dizer que:
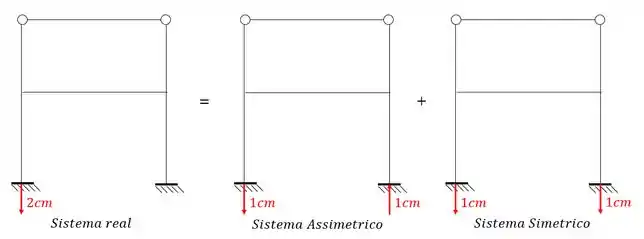
E assim cumprimos o primeiro objetivo do problema.
Passo 2
O segundo objetivo é determinar a estrutura simplificada, e para isso precisamos lembrar a nossa regrinha.
Se olharmos cada estrutura separadamente podemos determinar, dessa maneira temos que:
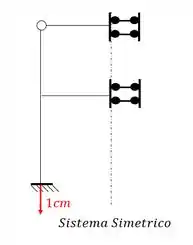
- Estrutura simétrica
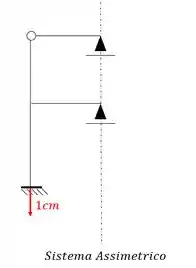
- Estrutura Assimétrica
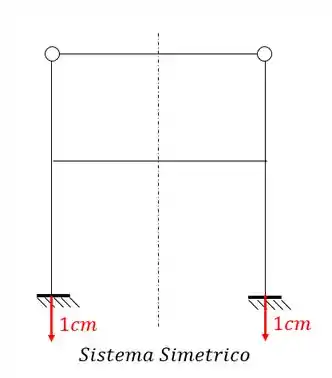
Perceba que o eixo de simetria corta apenas um ponto de cada barra, e se corta apenas um ponto, e faz parte do ramo simétrico, então trocamos metade por um carrinho, sendo assim a nossa estrutura será:
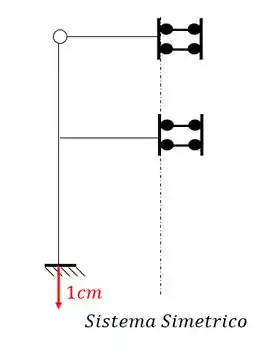
Porém perceba que a estrutura simétrica afunda como um todo 1cm, ou seja, não ocorrem recalques diferenciais (recalques diferentes em apoios diferentes) que são os tipos de recalques que geram momentos fletores. O que isso significa? Muito simples, se os recalques diferencias geram momentos fletores, e no caso simétrico não existem recalques diferenciais, então não temos momentos fletores devido a parcela simétrica, significando que devemos apenas resolver a parte assimétrica para determinar os momentos fletores na nossa estrutura.
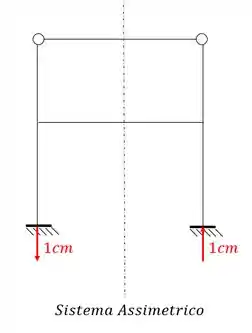
Perceba que o eixo de simetria corta apenas um ponto de cada uma das barras, e se corta apenas um ponto, e faz parte do ramo assimétrico, então trocamos metade por um apoio do primeiro gênero, sendo assim a nossa estrutura será:
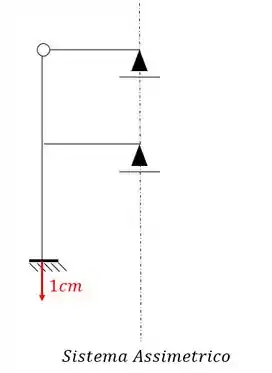
E perceba o seguinte, na parte de cima temos um apoio do primeiro gênero e uma rótula. Sabemos que o somatório de momentos em uma rotula deve ser zero, logo, se fizermos o somatório de momentos vindo pelo apoio mais a direita dela, veremos que não tem nenhum carregamento que pudesse anular a reação desse apoio, sendo assim, a única forma da reação desse apoio ter somatório zero na nossa rótula, é se o próprio valor da reação for zero. Mas porque estou falando isso? Porque se a reação desse apoio é zero, sabemos que tudo que faz parte da parte superior do nosso sistema pode ser desprezado, sendo assim a nossa estrutura assimétrica mais simples passa a ser:
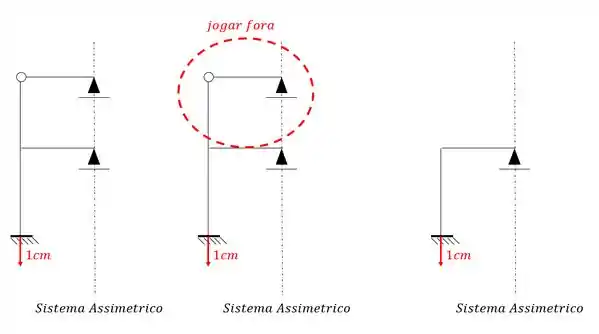
Passo 2
Agora precisamos resolver o nosso sistema hiperestático mais simples que sobrou. Lembrando que a nossa parte simétrica não apresentará contribuições, e por isso de cara descartamos ela. Sabido isso vamos lá:
Nossa estrutura a ser analisada é:
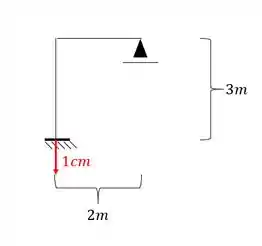
Temos um apoio do primeiro gênero e um do terceiro, totalizando assim 4 incógnitas.
Temos 3 equações de equilíbrio, e isso nos dá então 1 hiperestático a ser determinado.
Vou quebrar o vínculo de momento do apoio de terceiro gênero, e assim o nosso sistema passa a ser:
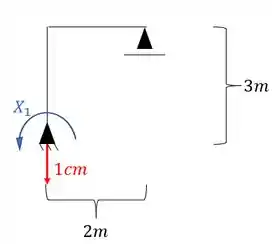
Sabemos que para resolver essa estrutura precisamos resolver o seguinte sistema:
Passo 3
Sabemos que para resolver precisamos usar a seguinte equação:
Em que basta aplicarmos na mesma posição e sentido do hiperestático uma carga unitária, determinar as reações de apoio, e com isso, calcular o valor de , sendo assim teremos que:
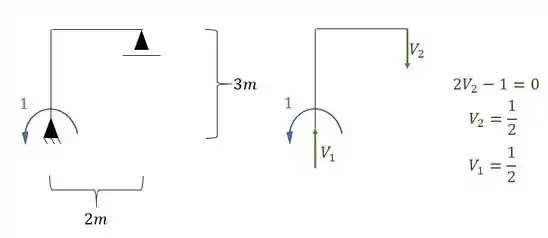
Como já sabemos o recalque ocorre no apoio mais a esquerda, e vale 1cm para baixo, como sabemos, se o recalque e a reação possuírem sentidos contrários, o sinal entre eles será negativo, sendo assim teremos que:
Passo 4
Sabemos que para resolver precisamos usar o hiperestático com valor unitário, mas determinar o diagrama de momentos fletores, e combinar os diagramas de momentos fletores, com os próprios diagramas de fletores. Senso assim, os nossos diagramas serão:
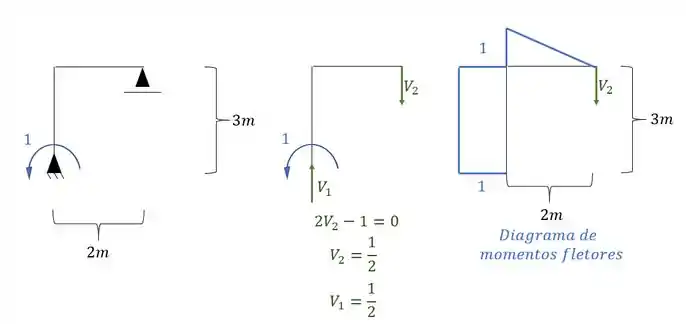
Combinando o diagrama unitário com o diagrama unitário, teremos que:
Sabendo que . Sendo assim teremos que:
Substituindo no nosso sistema teremos que:
Passo 5
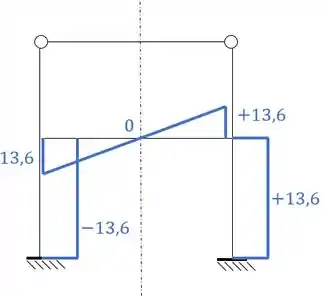
Para determinar o diagrama de momentos fletores basta lembrar que não possuímos diagrama no sistema zero que possui o recalque, mas temos no sistema com a carga unitária, sendo assim teremos que:
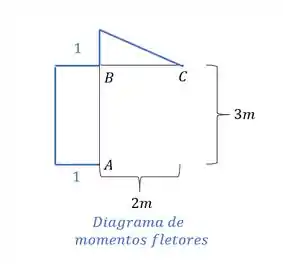
Se desenharmos metade do diagrama teremos que:
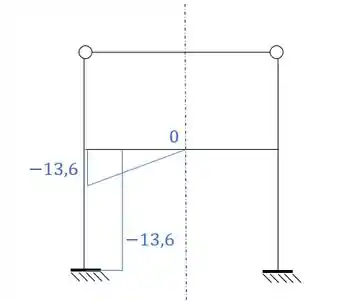
Porém lembre-se que desenhamos metade do diagrama ASSIMÉTRICO. Ou seja, se quisermos saber a outra metade, precisamos replicar a primeira metade mudando o sinal, dessa maneira teremos que:
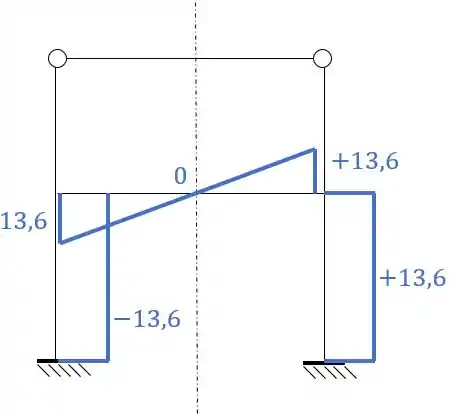
Resposta
A estrutura separada