Para a estrutura abaixo utilize o arranjo de cargas para separar, a partir do carregamento principal, a estrutura com carregamento simétrico e carregamento antissimétrico. Além disso, determine a estrutura mais simples a ser resolvida tanto para o caso simétrico quanto para o caso assimétrico.
Passo 1
Faaala, pessoal, vamos resolver um exerciciozinho sobre estruturas hiperestáticas? Vamos né! kkk
Esse problema pede, especialmente, que utilizemos o método do arranjo de cargas de forma a facilitar a resolução. Esse método consiste em manipular nossa estrutura de forma a obtermos duas estruturas que são mais fáceis de serem resolvidas.

Para fazer isso nós precisamos dividir a estrutura e os carregamentos em simétricos e antissimétricos e depois cortar cada estrutura na metade. Olha só!
Passo 2
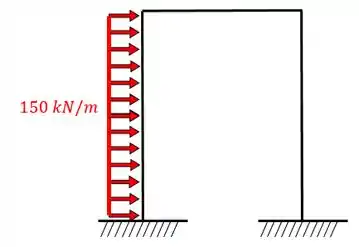
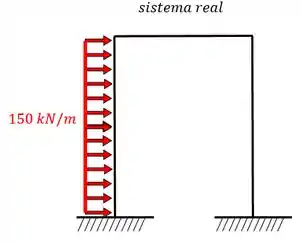
Então a primeira coisa é dividir o carregamento, antes nós tínhamos o sistema real:
Agora vamos dividir em dois sistema que somados são iguais ao real:
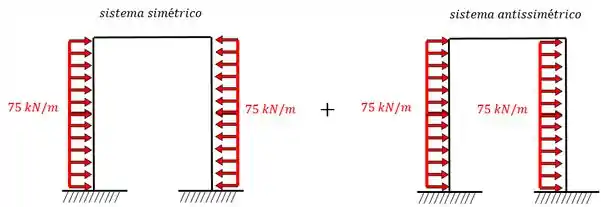
Olha como a carga das barras da esquerda quando somadas resultam em . Já as cargas das barras da direita quando somadas se anulam.
Pronto, esse passo está terminado!
Passo 3
Agora a gente vai cortar cada estrutura (simétrica e antissimétrica) e utilizar apenas uma metade. Aqui a gente só tem que lembrar que cada estrutura vai reagir de uma forma diferente:
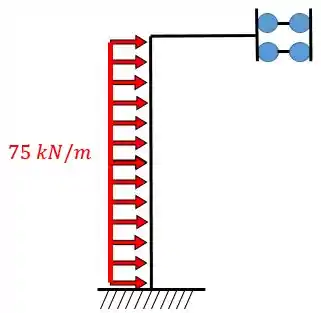
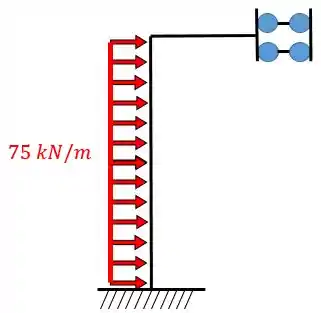
- Uma barra numa estrutura simétrica quando cortada deve possuir um engaste do tipo “carrinho”.
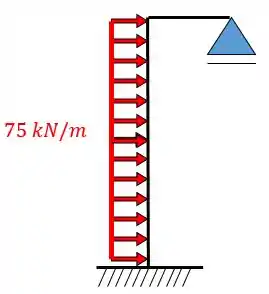
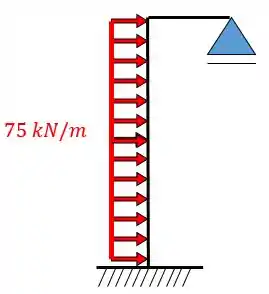
- Uma barra numa estrutura antissimétrica quando cortada deve possuir um apoio de primeiro gênero.
Fazendo o corte da estrutura simétrica:
Fazendo o corte da estrutura antissimétrica:
Pronto! A questão pede só isso, para separarmos cada estrutura! Perceba que o problema se tornou mais fácil porque nós conseguimos reduzir o grau de liberdade da estrutura. Nós ainda temos duas estruturas hiperestáticas mas elas são menos complexas do que a estrutura principal.
Resposta
A estrutura separa é:
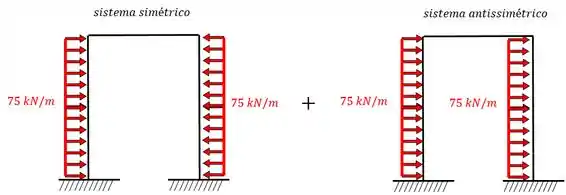
E as estruturas a serem resolvidas são:
- Simétrica
- Antissimétrica