Reduza cada um dos circuitos na figura a um único resistor nos terminais .
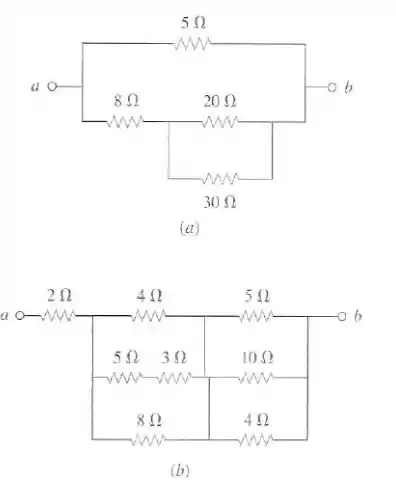
Passo 1
a) Aqui a ideia é:
- Paralelo do de com o de ;
- Série do de com o resultante do anterior;
- Paralelo do anterior com o de ;
Logo:
Depois:
Aí:
Passo 2
b) Já aqui, a ideia é a seguinte:
- Série nos resitores de e da parte da esquerda do circuito;
- Paralelo entre os 3 resistores da direita do circuito;
- Paralelo entre os 3 resistores da esquerda do circuito;
- Série entre os 3 resistores resultantes.
Bora lá:
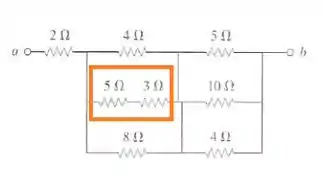
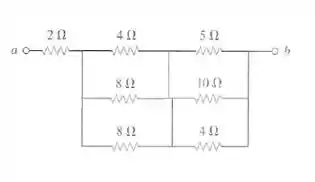
Depois:
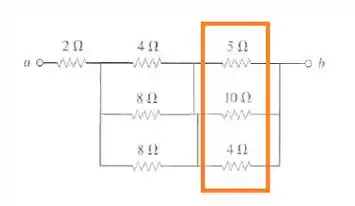
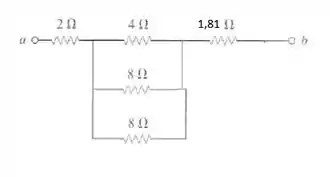
E então:
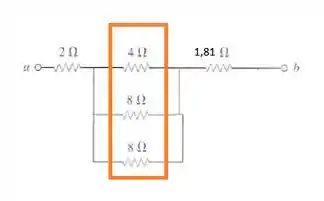
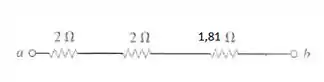
E finalmente:
Resposta
a)
b)