O é um gás que se decompõe de acordo com a reação estequiométrica:
A variação da concentração de com o tempo a 300 °C é dada por:
a) Verifique por método gráfico se a reação é de primeira ordem ou de segunda ordem.
b) Qual o tempo de meia vida para esta reação nas condições dadas?
c) Qual será a concentração de oxigênio após 400 segundos?
Passo 1
a)Em reações de primeira ordem:
Considerando , podemos simplificar para:
Portanto, podemos testar se uma reação é de primeira ordem traçando o gráfico de vs ou vs .
Em ambos os casos, caso a reação seja de primeira ordem, obteremos retas.
A diferença serão os coeficientes:
Vamos testar pela segunda equação. Você pode fazer com aquela que preferir!
Passo 2
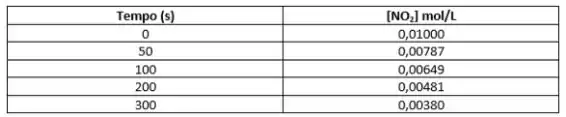
Primeiro, preparamos os pontos:
Tal que:
![]()
O que nos leva ao seguinte gráfico:
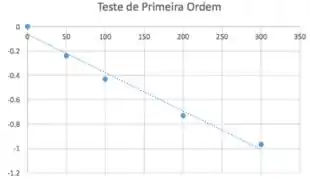
Cujos pontos se adequam mal a uma reta!
Vamos testar ela como de segunda ordem pra ver se ela se adequa melhor?
Passo 3
Para reações de segunda ordem:
Considerando :
Portanto, em reações de segunda ordem, obtemos uma reta ao traçar o gráfico de vs .
Bora lá!![]()
Que forma o gráfico:

Agora sim, temos uma reta!
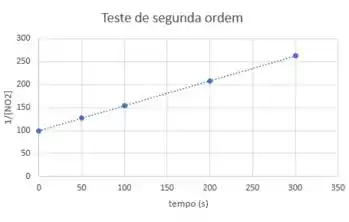
Como o gráfico de vs se adequa melhor a uma reta do que o gráfico de vs , a reação é de segunda ordem!
Passo 4
b) Para reações de segunda ordem, a meia vida depende da concentração inicial.
Dadas as condições iniciais do problema, o tempo transcorrido até que a concentração do reagente caísse pela metade pode ser definido pela reta que traçamos!
Quando:
Temos:
Assim:
O correspondente a será o .
E para descobri-lo, precisamos da equação da reta:
Onde:
E, pelo gráfico, vamos definir:
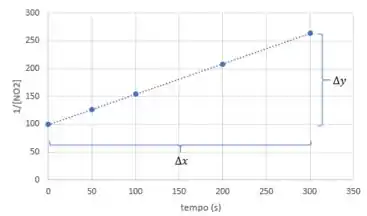
E para uma equação de segunda ordem, a unidade da constante é:
O que nos leva a seguinte equação da reta:
Tal que, para:
Teremos:
Passo 5
c) Atenção! Na letra c, o enunciado pede a concentração de OXIGÊNIO!
Vamos começar calculando a de :
Para :
Portanto, a quantidade consumida de foi de:
Como, a cada mol de consumidos, formamos meio mol de , podemos dizer que a concentração de após 400 segundos (considerando um recipiente fechado e tal), será:
Resposta
a) Segunda ordem.
b) 184,16 s.
c) 0,003425 mol/L.