Mínimos Quadrados - Caso discreto e contínuo
Produzido por Bruno PestanaTeoria
Introdução
Fala Aíí!! Imagina se nos deparamos com um problema desses:
Observe os pontos da função
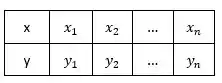
Com ,,..., pertencendo a um intervalo . Qual é a cara da função ?
Tremeu na base? Calma que eu tenho a solução para os seus problemas!!!
Vamos trabalhar com as informações que temos. Nesse caso só temos como base para achar a função os pontos dela, concorda?! Aqui que entra os Mínimos Quadrados! Através desse método vamos utilizar os pontos que temos para aproximar essa função o máximo que der e descobrir com qual carinha ela vai se parecer, beleza?!
Mínimos Quadrados
No tópico anterior nós vimos como resolver esse tipo de questão através do método dos Mínimos Quadrados. Vamos relembrar o que foi dito?!
Se quisermos resolver uma questão como a do enunciado, precisamos ESCOLHER funções ,,..., contínuas em e ENCONTRAR os coeficientes , , … , de modo que a função
Seja
Show de bola?!
Ou seja, a função vai se aproximar ao máximo de .
Primeiro precisamos analisar o gráfico de dispersão e encontrar as funções ,,..., contínuas em que mais se assemelham ao gráfico. Por exemplo, se tivermos esse gráfico:
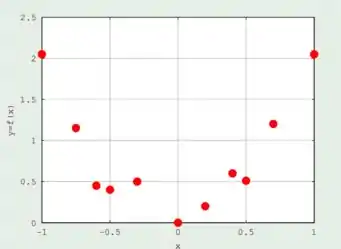
Esses pontos lembram pontos de uma parábola, concorda?! Então,
Podemos seguir o algoritmo apresentado no tópico anterior para encontrar os coeficientes
, , … , :
Passo 1. Dados iniciais (o que seu programa vai receber de você):
a. Vetor de valores
b. Matriz com os vetores
Passo 2. Definimos como uma matriz cheia de zeros.
Passo 3. Definimos como um vetor de tamanho cheio de zeros.
Passo 4. Para de a repita o passo 5.
Passo 5. Para de a repita o passo 6.
Passo 6.
Passo 7. Para de a repita o passo 8.
Passo 8.
Passo 9. Jogamos nossa matriz e nosso vetor em algum método de resolução linear e teremos como retorno o vetor dos coeficientes .
E é assim que aprendemos a resolver esse tipo de questão, mas isso só aplica a casos discretos.

Caso discreto? WTF?! Calma que você já vai entender!
O método de interpolação por mínimos quadrados acontece com dois casos: o caso discreto e o caso contínuo.
O caso discreto, que já sabemos resolver, é o caso onde o enunciado da questão nos dá pontos de uma função (que pode ou não ser contínua) e nós achamos uma aproximação.
Já no caso contínuo, o enunciado nos dá uma função CONTÍNUA em um intervalo e nos pede uma aproximação.
Se olharmos novamente para o enunciado, foram fornecidos pontos de uma função que não sabemos se é contínua ou não... então resolvemos através do Método dos Mínimos Quadrados Caso Discreto!

Vamos aprender agora como faz para encontrar o uma aproximação através do Método dos Mínimos Quadrados Caso Contínuo?!
Mínimos Quadrados Caso Contínuo
Pra ficar mais claro vamos começar com um exemplo:
Encontre a reta que melhor aproxima em
Percebe que o enunciado está pedindo para aproximar uma função polinomial? Sabemos que funções polinomiais são contínuas nos reais e sabemos calcular todas as suas derivadas e integrais…
Mas e se eu te perguntar o gráfico dela? Difícil de imaginar né? Confesso que eu não tenho a mínima ideia também... por isso que faz sentido querermos aproximar essa função para uma coisa mais fácil de trabalhar, como uma reta!!
Tá beleza, mas como fazemos isso? Vamos descobrir agora!

Ok, imagina que temos que aproximar uma função contínua .
Da mesma forma do caso discreto, queremos encontrar uma função tal que
sendo que:
Como se trata de uma função contínua, para o erro ser menor, calcular essa função significa que queremos que a área sob a curva do quadrado dos desvios seja mínima, ou seja estamos falando agora de integrais:
Beleza?!
Ok, então já sabemos o que queremos. Agora, da mesma forma que no caso discreto, vamos encontrar os pontos críticos de , nos quais a derivada é zero:
Para todo .
Se substituímos o valor de e calcularmos a derivada parcial pela regra da cadeia obteremos isso:
Como queremos , temos:
Se quiser ainda podemos abrir a integral desse jeito:
Para todo
Essa é a equação geral na hora de resolver o problema! Você tem que encontrar uma equação para cada que tiver. No final você vai ter um sistema de equações desse jeito:
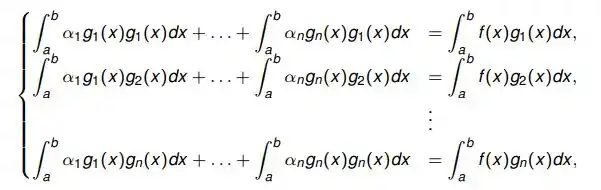
Esse sistema é chamado se sistema de equações normais, beleza?!
Respira fundo que tá acabando!

Ok, da mesma forma do caso discreto, precisamos ESCOLHER funções ,,..., contínuas em e ENCONTRAR os coeficientes , , … , .
As funções ,,..., vão depender do enunciado e para o quê queremos aproximar essa função . Então só falta agora entender como encontrar os coeficientes , , … , .
Vamos seguir os mesmos passos do caso discreto, escrever o sistema de equações normais em forma matricial:
De modo que:
- seja uma matriz,
- a matriz com os coeficientes
A matriz será definida como:
E como:
Resolvendo esse sistema de matrizes conseguimos encontrar o valor de cada coeficiente da função
Vamos agora fazer aquele exemplo para tudo ficar claro como a luz do sol?!

Exemplo
Encontre a reta que melhor aproxima em.
Ok, temos aqui uma função Polinomial de grau três que queremos aproximar para uma reta.
Se queremos aproximar para uma reta, cara da nossa vai ser:
onde:
e
Beleza?!
Porque desse modo obtemos uma equação de reta
Show de bola?!
Agora vamos calcular nossa matriz
E assim encontramos o elemento da nossa matriz A.
Para encontrar os próximos elementos da matriz é só seguir a mesma idéia.
Se você reparar nesse caso ,
Agora só falta encontrar
Calculando temos:
Tudo pronto para montar nosso sistema matricial!
Resolvendo o sistema, encontramos os valores dos coeficientes:
Chegamos na resposta para o problema!! \o\
A função que melhor aproxima em em uma reta é:
Viu, é mais fácil que parece! Bora fazer mais exercícios :)
Mínimos Quadrados Caso Contínuo
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
Material Cálculo numérico ICMC- Caso discreto
Utilizando o método discreto, obtenha a reta que melhor se ajusta ao seguinte problema:
![]()
Passo 1
Temos que encontrar a reta que se ajusta bem aos pontos e resolve o sistema .
Considerando os dados:
![]()
Vamos montar uma daquelas famigeradas tabelinhas mágicas para resolver o sistema, contendo os seguintes somatórios: :
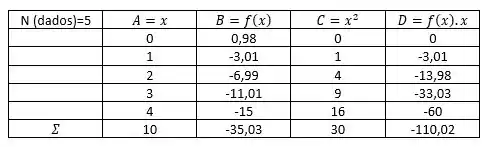
Com esses dados, conseguimos montar um sisteminha com os dados encontrados:
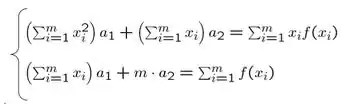
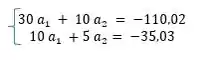
Solucionando o sistema, ficamos com:
Resposta
Exercício Resolvido #2
Material Cálculo numérico ICMC- Caso discreto
Utilizando o método discreto, obtenha a reta que melhor se ajusta ao seguinte problema:

Passo 1
Temos que encontrar a reta que se ajusta bem aos pontos e resolve o sistema .
Considerando os dados:

Vamos montar uma daquelas famigeradas tabelinhas mágicas para resolver o sistema, contendo os seguintes somatórios: :
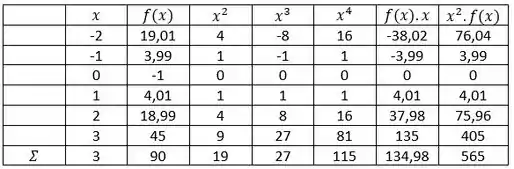
Com esses dados, conseguimos montar um sisteminha com os dados encontrados:
Passo 2
Solucionando o sistema por qualquer um dos métodos de resolução de sistemas lineares.
Link do programa: https://matrixcalc.org/pt/slu.html
Para facilitar a visualização, usaremos um programa que soluciona sistemas lineares pelo método de Gauss, que já vimos anteriormente e nosso objetivo aqui é entender o método dos mínimos quadrados!
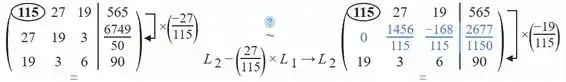

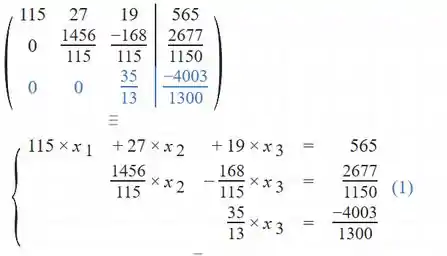
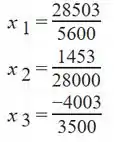
Resposta
Exercício Resolvido #3
Adaptado do material aula 18- Ime Unicamp
Encontre a reta que melhor se aproxima do polinômio em.
Passo 1
Para encontrar a reta que melhor se aproxima do polinômio, fazemos considerações iniciais:
A reta que irá se aproximar melhor do polinômio é:
Passo 2
Aqui, montaremos a nossa matriz e sistemas de equações partindo das integrais no intervalo dado:
Passo 3
A partir desses dados, montamos o sisteminha de equações:
Resolvendo o sistema, ficamos com:
Resposta
O polinômio interpolador é:
Exercício Resolvido #4
Autoria do Responde Aí
O diagrama de dispersão é extremamente importante para definir qual será o comportamento de um conjunto de pontos e escolher qual tipo de ajuste de curvas se encaixa melhor. Programe, hipoteticamente, um mecanismo que armazene pontos e imprima na tela no formato de diagrama de dispersão e só para deixar divertido, escolha uma cor para o diagrama:
Passo 1
Aqui, usaremos como base a lógica de programação utilizada no octave e matlab :
Primeiro dizemos o que é o nosso programa e para que serve, o disp imprime na tela e não armazena dados
disp ('O programa realiza o ajuste linear de curvas usando o metodo dos minimos quadrados.');
Agora, colocamos uma mensagem para que o usuário digite, mas precisamos que sejam armazenados valores:
n=input('Digite a quantidade de termos do vetor x maior que 1 : '); %
O mesmo valore para valores de y:
m=input('Digite a quantidade de termos do vetor y maior que 1 : '); % em tese o vetor y deve ter o mesmmo tamanho de x para todas, essa linha existe apenas por causa do error
Definimos uma condição de erro, para que x e y tenham tamanho igual:
if n!=m %Da uma condição, que se for verdadeira executa um comando error("Programa indevido.\n"); %função error, define um erro se o tamanho dos vetores x e y forem errados (condição anterior)
endif %Finaliza a condição executada
Passo 2
Definir as entradas:
x=0; %definir como zero para entrar no laço de repetição
y=0; %%definir como zero para entrar no laço de repetição
Trabalharemos com o x, imprimindo recados ao usuário e ao computador para armazenar os dados:
disp ('Valores para o vetor x ') %Imprime para o usuário quais valores ele vai precisar inserir no programa for i = 1:n %n é o tamanho maximo de dados do vetor
x(i)= input('Digite o valor: '); %valores que o x vai receber e armazenar endfor %finaliza o laço de repetição
O mesmo vale para y:
disp ('\nValores para o vetor y') %Imprime que tipo de valor o usuário vai colocar no programa for i = 1:n %tamanho maximo no vetor y deve ser o mesmo de x
y(i)= input('Digite o valor: '); %valores recebidos por y endfor %finaliza o laço de repetição
Passo 3
Agora vamos ao diagrama de fato:
Devemos definir o diagrama como figura
figure
Agora, colocamos a função do diagrama:
scatter (x,y, 'm') %plota diagrama de dispersão, 'm' muda a cor para magenta
Resposta
scatter (x,y, 'm') %plota diagrama de dispersão, 'm' muda a cor para magenta
Exercício Resolvido #5
Autoria do responde Aí
Relacione A para método dos mínimos quadrado de caso discreto e B para o caso contínuo:
( ) Utiliza diagrama de dispersão.
( ) Necessita de um conjunto de pontos
( ) Se o determinantedo sistema de equações normais for diferente de zero, então há um ajuste único de parâmetros que minimiza o erro quadrático.
( ) Quando as funções escolhidas (g_1, g_2...g_n) forem linearmente independentes, o determinante será diferente de zero
( ) Utiliza cálculo de integrais no processo.
Passo 1
- Utiliza diagrama de dispersão.
O método do caso discreto analisa e direciona o cálculo através da análise gráfica do diagrama de dispersão.
Passo 2
(A) Necessita de um conjunto de pontos
Passo 3
( B ) Se o determinantedo sistema de equações normais for diferente de zero, então há um ajuste único de parâmetros que minimiza o erro quadrático.
( B ) Quando as funções escolhidas (g_1, g_2...g_n) forem linearmente independentes, o determinante será diferente de zero
( B ) Utiliza cálculo de integrais no processo.
Resposta
Relacione A para método dos mínimos quadrado de caso discreto e B para o caso contínuo:
(A) Utiliza diagrama de dispersão.
(A) Necessita de um conjunto de pontos
(B) Se o determinantedo sistema de equações normais for diferente de zero, então há um ajuste único de parâmetros que minimiza o erro quadrático.
(B) Quando as funções escolhidas (g_1, g_2...g_n) forem linearmente independentes, o determinante será diferente de zero
(B) Utiliza cálculo de integrais no processo.