Caso Não Linear
Teoria
Introdução
Faaaaala aí, tudo certinho? Vamos dar uma recapitulada: até agora nós vimos ajuste linear de uma função, mas e se a função tiver um comportamento muito diferente, dá pra usar o método dos mínimos quadrados?
Muitas vezes, nós temos dados experimentais em que o ajuste linear não é adequado e não pode ser considerado. Neste caso, necessitamos de outras famílias de funções que representem bem o conjunto de dados.
Agora um dos parâmetros foi para dentro da função e não é mais linear. E agora, o que fazemos?
O Responde Aí, é claro! Então vamos ver como prosseguir nesses casos.
Caso não linear
O primeiro caso é o ajuste exponencial, se nós obtemos os dados experimentais dispostos como uma exponencial a qual sugere que devemos aproximar. A dificuldade de aplicação do método dos mínimos quadrados neste caso consiste na tentativa de minimizar o erro. Considerando a e b constantes, temos a função:
Aplicando logaritmo dos dois lados temos:
Substituindo:
Com todas essas considerações, nós conseguimos:
Que é um problema que sabemos resolver pois é linear!! Não contavam com a nossa astúcia! Vamos ver um exemplo de como isso funciona na prática.
Suponha que você obteve a tabela de abaixo de uma experiência:
Se jogarmos isso em um diagrama no diagrama de dispersão temos:
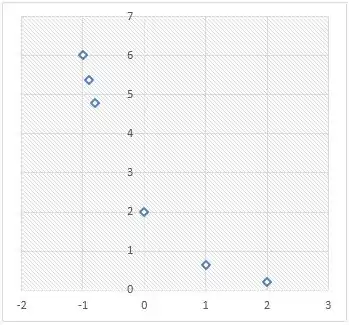
Que parece ser uma exponencial decrescente então vamos aproximar com essa função aqui:
Agora reescrevemos a tabela trocando por que é o nosso :
Se jogarmos novamente esses pontos em um diagrama de dispersão, teremos:
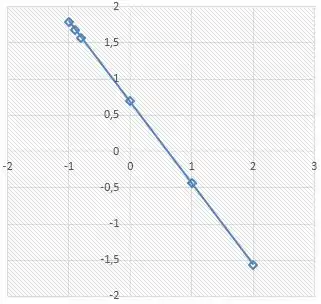
E como já era de se esperar, temos uma reta! Se a nossa aproximação não for razoável, o que nesse exemplo quer dizer que os pontos não se comportam como uma função da família , esse diagrama de dispersão não daria uma reta! Esse diagrama é o chamado teste de alinhamento e serve para verificarmos se escolhemos uma boa família de funções para aproximar os pontos da tabela.
A menos que o exercício peça, ele é opcional, você faz se quiser pra ter certeza que ta indo no caminho certo. Agora a gente resolve normalmente usando:
Vamos montar aquela tabela de organização, e a primeira e segunda coluna são basicamente o que o exercício dá, então é só preencher e . Para cada linha da tabela iremos preencher também cada valor de elevado ao quadrado, e também cada valor de multiplicando pelo valor da função no ponto . . Pra fazer o somatório, basta somar os valores totais de caaaaaada coluna.
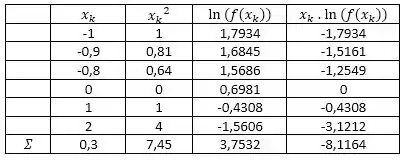
Reorganizando direitinho, as fórmulas para são:
Jogando na fórmulinha aqueles valores que nós organizamos na tabela fica:
Agora lembrando das trocas de variáveis que a gente fez, temos que:
Assim, nossa função é:
Show? E só pra mostrar pra vocês que realmente funciona olha como essa função que a gente encontrou se ajeita aos pontos:
É tão bonito quando as coisas funcionam né? haha.
Casos Comuns
Bom, naturalmente a forma que você vai usar para linearizar a função vai depender muito do problema, mas vou mostrar pra vocês algumas linearizações manjadas ;)
1. Hiperbólica
2.Exponencial
3.Potencial
Nesse caso, para tornar a função completamente linear podemos fazer uma outra mudança de variável , obtendo . Isso é opcional pois como sabemos podemos aplicar o método dos mínimos quadrados em funções como .
Algoritmo
Não tem algoritmo aqui porque a linearização que você vai fazer depende do problema e, portanto, não existe um algoritmo geral. Depois de fazer a linearização é só jogar no algoritmo dos mínimos quadrados que vimos no último tópico
Vamos fazer uns exercícios pra fixar então!
Casos Comuns
Algoritmo
Exercícios Resolvidos
Exercício Resolvido #1
Lista 5 – Professora Angela – UFRJ – Questão 3
A tabela abaixo representa o consumo de um novo produto em determinada cidade, durante o ano de . Admitindo-se que o aumento do consumo é exponencial, estime o consumo para agosto usando o Método dos Mínimos Quadrados. (consumo )
Passo 1
Se dissermos que o mês é nossa variável , que o consumo é uma função de e usarmos os números correspondentes de cada mês ficamos com:
Onde nossa função de aproximação é:
Linearizando:
A tabela linearizada fica assim:
E temos que e .
Temos então os vetores:
Passo 2
Agora montamos a matriz que vai ser já que temos duas funções :
E o vetor :
Resolvendo o sistema:
Voltando as variáveis:
Logo:
Substituindo para o mês :
Ou seja, aproximadamente unidades.
Resposta
unidades
Exercício Resolvido #2
Lista 5 – Professora Angela – UFRJ – Questão 4
A tabela abaixo representa a intensidade de uma fonte radioativa. Determinar a intensidade de radiação para usando ajuste exponencial.
Passo 1
Nossa aproximação será
Linearizando:
A tabela linearizada fica assim:
E temos que e .
Temos então os vetores:
Passo 2
Agora montamos a matriz :
E o vetor :
Resolvendo o sistema:
Voltando as variáveis:
Logo:
Passo 3
Substituindo para :
Resposta
Exercício Resolvido #3
UNICAMP – Lista 6 – Questão 9 Adaptada
Verifique que as funções não lineares a seguir podem ser linearizadas por transformações matemáticas. Explicite a relação entre a função original e a linearizada.
Passo 1
Então a função linearizada é a seguinte:
Com relações:
Passo 2
A função linearizada é:
Podemos ainda fazer a mudança de variáveis obtendo , apesar de podermos resolver o problema sem essa mudança.
Com relações:
Passo 3
A função linearizada é:
Novamente podemos fazer a mudança de variáveis obtendo .
Com relações:
Resposta
; ;
; ; ;
; ; ;
Exercício Resolvido #4
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 290, exercício 10 Adaptado
Aproxime a tabela abaixo por uma função do tipo usando quadrados mínimos. Encontre o erro da aproximação.
Passo 1
Nossa aproximação será
Linearizando:
A tabela linearizada fica assim:
E temos que e .
Temos então os vetores:
Passo 2
Agora montamos a matriz :
E o vetor :
Resolvendo o sistema:
Voltando as variáveis:
Logo:
Passo 3
Agora para encontrarmos o erro, também conhecido como o resíduo, basta calcularmos:
Resposta
Erro:
Exercício Resolvido #5
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 290, exercício 11
Considere a tabela
Por qual das funções ou você aproximaria a função ? Justifique sua resposta.
Passo 1
Lembra do teste que eu comentei pra ver se escolhemos a família certa de funções? O teste do alinhamento! Primeiro vamos linearizar ambas as funções:
Isso nos dá a tabela abaixo:
Repare que usando essa função como aproximação esbarramos com um problema! Nossa linearização não está definida em . Como se não bastasse isso, se jogarmos os pontos em um diagrama de dispersão vamos ficar com isso aqui:
Nada a ver com uma reta essa porcaria né?
Passo 2
A outra aproximação fica:
O que nos dá a tabela abaixo
E o diagrama de dispersão dessa tabela nos dá:
Po, não vou dizer que está uma reta perfeitinha, mas está infinitamente melhor que o outro haha. E aqui a gente não tem o problema da indeterminação em um ponto! Logo, a melhor função para aproximar a é .
Resposta
aproxima melhor a função pelo teste do alinhamento. Além disso, a linearização de possui uma indeterminação em um dos pontos tabelados.