Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios complementares - Ex. 29

Considere a integral:

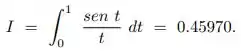
Mostre que o resultado obtido pela regra 1 3 de Simpson com h = 0.5 é surpreendente próximo do resultado exato. Explique por que isso acontece. (sugestão: analise o erro).

Passo 1

Eaii! Bora para mais uma questão. Aqui teremos que verificar se de fato o resultado obtido é próximo ao resultado exato e então, através do erro, validar as afirmações do enunciado.Vamos considerar o erro da regra 1 3 de Simpson:

𝑒   =   − 𝑛 90 h 5 𝑓 𝑖 𝑣 𝑡 ,   𝑡   ∈   𝑎 , 𝑏

Observe que h é o passo, 𝑓 𝑖 𝑣 𝑡 é a quarta derivada da função no ponto que maximiza a função.

Passo 2

Calculando a quarta derivada de 𝑠 𝑒 𝑛   𝑡 𝑡 , obtemos:

𝑠 𝑒 𝑛   𝑡 𝑡 ′ ′ ′ ′   = 𝑡 4 𝑠 𝑒 𝑛 𝑡 + 4 𝑡 3 c o s c o s   𝑡   − 3 𝑡 2 𝑠 𝑒 𝑛 𝑡 + 2 𝑡 c o s c o s   𝑡   − 𝑠 𝑒 𝑛 𝑡   𝑡 5

Para t = 1, esse monstrinho é maximizado com o valor de aproximadamente 0.13 . Sabendo que o passo é 0.5 e o valor da derivada quarta maximizada é 0.13, verificamos que o erro será muito pequeno e por isso o valor ser surpreendente próximo faz sentido. Acabamos por aqui, beleza? Até mais!

Resposta

O erro é muito pequeno, por isso os valores são próximos!

Exercícios de Livros Relacionados

110. Seja f e g duas funções tais que para todo x em ( - ∞ ,+ ∞ ) , f ´ ( x )=g ( x ) e g ' x = - f ( x ) . Depois, suponha que f 0 = 0eg 0 = 1 . Prove que [ f x ] 2 + [ g x ] 2 = 1 Sugestão: consider
A tabela a seguir mostra dados de velocidade e tempo de um carro esporte que acelera do repouso para 130m i l h a s / h . Qual a distância percorrida pelo carro ao atingir essa velocidade? (Use trapéz
O projeto de um novo avião requer um tanque de gasolina com área de seção transversal constante em cada asa. Apresentamos o desenho em escala de uma seção transversal. O tanque deve conter 5000l b de
Determine, com precisão de duas casas decimais, as áreas das superfícies geradas pela rotação da curva ao longo do eixo x y =s e nx, x ∈ 0 , π