Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 9I

Resolver os exercícios 11.1 e 11.8 usando a regra de Simpson.

Passo 1

Eaí colega!! Tudo tranquilo? Vamos aprender a utilizar uma nova regrinha para calcular o valor numérico de integrais, que é a regra de Simpson, dada pela seguinte fórmulinha:

Sabendo disso, vamos apenas deixar claro aqui que o exercício foi dividido nos itens I e II, beleza? Neste item (I) iremos resolver o exercício 11.1, é para calcular a seguinte integral:

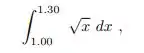
Seguindo a tabela:

Passo 2

Agora basicamente precisaremos encontrar o passo (h) e fazer os cálculos. Para isso, considere que vamos nomear cada intervalo, x = 1 será o intervalo 0, x = 1.05 será o intervalo 1, e assim por diante ok?Apropiando a fórmula, ficamos com:

Agora só é necessário substituir os valores e vamos obter:

Note que usamos o valor do passo (h = 0.05) que foi o mesmo passo que usamos no exercício 1.

Resposta

O valor da integral foi aproximadamente .

Exercícios de Livros Relacionados

Use a regra de simpson para aproximar a área da região sombreada na figura.

31 - Integrais elípticas - O comprimento da elipse: x 2 a 2 + y 2 b 2 = 1 vem a ser: C o m p r i m e n t o =4 a ∫ 0 π 2 1 - e 2 cos 2 ⁡ t d t onde e = a 2 - b 2 a é a excentricidade da elipse. A integ

32 - O comprimento de um arco da curva y = sen x é dado por: L = ∫ 0 π1 + cos 2 ⁡ x Estime L pela regra de Simpson com n = 8.

Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ - 1 1 ( x 2 + 1 ) d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson