Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios complementares - Ex. 27

Nas integrais do exercício anterior com quantas divisões do intervalo, podemos esperar obter erros menores que 10 − 5 ?

Passo 1

Opa! Bora para mais um! Vamos relembrar as fórmulas dos erros para podermos calcular o número de intervalos que precisamos para obter erros menores que 10 − 5 .

Trapézio:

10 − 5 ≥ − h 3 12 𝑓 ′ ′ 𝑡 ,   𝑡   ∈   𝑎 , 𝑏

1 3 de Simpson:

10 − 5 ≥ − h 4 𝑏 − 𝑎 180 𝑓 𝑖 𝑣 𝑡 ,   𝑡   ∈   𝑎 , 𝑏

3 8 de Simpson:

10 − 5 ≥ − 3 80 h 5 𝑓 𝑖 𝑣 𝑡 ,   𝑡   ∈   𝑎 , 𝑏

Passo 2

Considerando as integrais do exercício anterior:

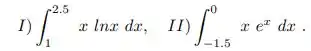
Para a integral I, teremos as seguintes derivadas:

𝑥 l n l n   𝑥   ′ ′   =   1 𝑥

𝑥 l n l n   𝑥   ′ ′ ′ ′   =   2 𝑥 3

Já para a integral II:

𝑥 𝑒 𝑥 ′ ′   = 𝑥 𝑒 𝑥   + 2 𝑒 𝑥

𝑥 𝑒 𝑥 ′ ′ ′ ′   = 𝑥 𝑒 𝑥 + 4 𝑒 𝑥

Com isso é só substituir na fórmulinha para o valor do intervalo que maximiza a função. Com todos os cálculos feitos, chegaremos em:

Para a integral I:Aproximadamente 200, 10 e 12 divisões para a regra do trapézio, 1 3   e 3 8 respectivamente.

Para a integral II:

Aproximadamente 240, 12 e 12 divisões para a regra do trapézio, 1 3 e 3 8 respectivamente.

Fechamos aqui!! Até mais.

Resposta

I) 200, 10 e 12 divisões para a regra do trapézio, 1 3 e 3 8 , respectivamente.

II) 240, 12, 12 divisões para a regra do trapézio, 1 3 e 3 8 , respectivamente.

Exercícios de Livros Relacionados

Determine, com precisão de duas casas decimais, as áreas das superfícies geradas pela rotação da curva ao longo do eixo x y = x 2 4, x ∈ 0 , 2
Sua empresa de fabricação de metal está tentando fechar contrato para produzir folhas onduladas de metal para telhado, como mostramos a seguir. As seções transversais dessas folhas devem se ajustar à
Sua empresa de engenharia está tentando fechar contrato para a construção de um túnel, como o que mostra a figura a seguir. O túnel tem 300p é s é de comprimento por 50p é s é de largura na base. Sua
Uma piscina retangular tem 30p é s é de largura e 50p é s é de comprimento. A tabela a seguir mostra a profundidade h(x) da água em intervalos de 5p é s é de uma extremidade da piscina até a outra. Es
Prove que a soma T na regra do trapézio para ∫ a b f x d x é uma soma de Riemann para f contínua em [ a ,b ] . Dica: use o teorema do valor intermediário para mostrar a existência de c k no subinterva