Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 8.Problemas Aplicados e Projetos - Ex. 1

A tabela a seguir lista o número de acidentes em veículos motorizados no Brasil em alguns anos entre 1980 e 1998.

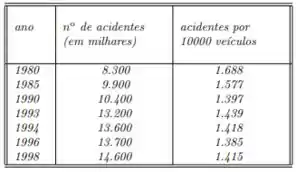
a) Calcule a regressão linear do número de acidentes no tempo. Use-a para prever o número de acidentes no ano . (Isto é chamada uma análise de série temporal, visto que ´e uma regressão no tempo e é usada para prognosticar o futuro).

b) Calcule uma regressão quadrática do número de acidentes por veículos. Use esta para prognosticar o número de acidentes por veículos no ano .

c) Compare os resultados da parte a) e b). Em qual delas você está mais propenso a acreditar?

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide A tabela a seguir lista o número de acidentes em veículos motorizados no Brasil em alguns anos entre 1980 e 1998.

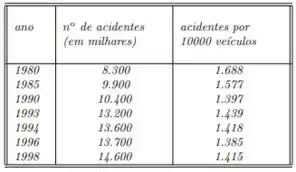
a) Calcule a regressão linear do número de acidentes no tempo. Use-a para prever o número de acidentes no ano . (Isto é chamada uma análise de série temporal, visto que ´e uma regressão no tempo e é usada para prognosticar o futuro).

b) Calcule uma regressão quadrática do número de acidentes por veículos. Use esta para prognosticar o número de acidentes por veículos no ano .

c) Compare os resultados da parte a) e b). Em qual delas você está mais propenso a acreditar?

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha seguindo a distribuição conforme os anos na tabela do passo acima temos que na letra (a) para calcular a regressão linear do número de acidentes do ano , temos

Já na letra (b) ele pede para calcular a regressão quadrática do número de veículos temos

E por fim na letra comparando os resultados de (a) e (b) podemos dizer que o caso (b) é o mais propenso a ser verdade pois seus valores condizem com o número de acidentes.

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

c) o caso (b) é o mais propenso a ser verdade pois seus valores condizem com o número de acidentes.

Exercícios de Livros Relacionados

O número de números primos menores que x é denotado por π ( x ) e vale a tabela:a) Determinar pelo método dos mínimos quadrados, para os dados acima, expressão do tipo: π x = a + b x log 10 ⁡ x b) Est

(Ajuste na curva tração/deformação de um tipo de aço). Feito um ensaio de tração em uma barra de um tipo de aço, em uma máquina universal de Amsler, foram obtidos os valores constantes da tabela a seg

Em uma floresta densa, dois formigueiros inimigos, separados por um rio, travam uma longa batalha. Um dos formigueiros, visando acabar gradativamente com a espécie inimiga, dá uma cartada fatal, seque

Os dados das tabelas a seguir mostram a quantidade de alcatrão e nicotina (em miligramas) para várias marcas de cigarro com e sem filtro i ) Calcule as regressões lineares do tipo a x + b para a relaç