Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 8.Problemas Aplicados e Projetos - Ex. 10

(Ajuste na curva tração/deformação de um tipo de aço). Feito um ensaio de tração em uma barra de um tipo de aço, em uma máquina universal de Amsler, foram obtidos os valores constantes da tabela a seguir. Deseja-se obter representações aproximadas para

Faça um gráfico dos dados. Observando o gráfico você ver à que deve fazer:

a) uma regressão linear para os primeiros pontos ;

b) uma regressão quadrática para os pontos seguintes

c) uma regressão linear para os últimos pontos

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide dado um ensaio de tração em uma barra de um tipo de aço, em uma máquina universal de Amsler, foram obtidos os valores constantes da tabela a seguir. Deseja-se obter representações aproximadas para

Faça um gráfico dos dados. Observando o gráfico você ver à que deve fazer:

a) uma regressão linear para os primeiros pontos ;

b) uma regressão quadrática para os pontos seguintes

c) uma regressão linear para os últimos pontos

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha nessa questão ele pede para determinarmos gráficos em cada item pedido, como na letra (a) em que ele pede a regressão linear de pontos com intervalo , ficando

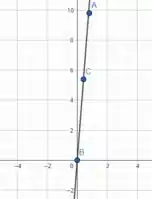
Já na letra (b) para a regressão linear de pontos e intervalo , ficando

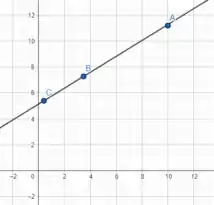
E por fim na letra para regressão linear nos últimos pontos temos

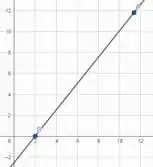
Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

a) gráfico demonstrado no passo anterior.

b) gráfico demonstrado no passo anterior.

c) gráfico demonstrado no passo anterior.

Exercícios de Livros Relacionados

Um modelo para o crescimento da população segundo Verhulst é que a população, P , cresce no tempo de acordo com a equação diferencial: d P d t = A - B P P O parâmetro A é a taxa geométrica de crescime

Seja a tabela:Usando interpolação linear sobre pontos adequados:a) Calcular f0.35 onde f x = x 2 . e x . b) Dar um limitante superior para o erro de truncamento.

O valor de log 10 ⁡ 12,7 foi computado por interpolação linear sobre os pontos 12e13 . Mostrar que o erro de truncamento é ≤ 0 , 004 .

Sabendo-se que 1,03 = 0 , 0149e1,04 = 1.0198 , a) calcular 1,035 , por interpolação linear; b) dar um limitante superior para o erro de truncamento.

Dada a função f ( x ) =4 x 5 -2 x+2 , tabelá-la nos pontos x = 0;x = ± 1;x = ± 2 e construir o seu polinômio de interpolação no intervalo [ - 2 ; 2 ] .