Em uma floresta densa, dois formigueiros inimigos, separados por um rio, travam uma longa batalha. Um dos formigueiros, visando acabar gradativamente com a espécie inimiga, dá uma cartada fatal, sequestrando a rainha. Para não ver seu formigueiro destruídos, algumas formigas guerreiras se unem com as formigas engenheiras numa arriscada operação de resgate à rainha. Mas como resgatá-la?
As formigas guias arquitetaram um plano de resgate que consistia em arremessar algumas formigas guerreiras, algumas formigas engenheiras, algumas guias e algumas operárias sobre o formigueiro inimigo. Chegando lá, elas dividiram-se em dois grupos. Um grupo composto pelas formigas guerreiras e formigas guias, incumbira-se de entrar no formigueiro inimigo em busca da rainha. O outro grupo, composto pelas formigas engenheiras e pelas formigas operarias, incumbira-se de fabricar uma catapulta que os arremessasse de volta ao seu formigueiro de origem. Para que nenhum imprevisto ocorresse quando do arremesso da rainha, as formigas engenheiras foram consultadas. Elas então criaram um modelo teórico de catapulta. A catapulta consistia em utilizar um pedaço de matinho de tamanho fixo. A rainha deveria ser colocada em uma ponta, com a catapulta inclinada em um determinado ângulo , e arremessada numa distância exata entre os formigueiros. No entanto, para que isso ocorresse, era necessário saber qual matinho usar. Algumas formigas então começaram a realizar testes com matinho de uma mesma espécie, mas com diferentes diâmetros e verificaram que, para um alcance horizontal fixo igual à distância entre os formigueiros, o ângulo de arremesso variaria com o diâmetro do matinho, segundo a seguinte tabela de dados:
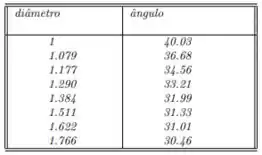
Para encontrar a melhor curva descrita por esses pontos as formigas engenheiras fizeram um programa que encontrava a melhor aproximação pelo método dos mínimos quadrados. Faça você o mesmo que as formigas engenheiras!
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide Em uma floresta densa, dois formigueiros inimigos, separados por um rio, travam uma longa batalha. Um dos formigueiros, visando acabar gradativamente com a espécie inimiga, dá uma cartada fatal, sequestrando a rainha. Para não ver seu formigueiro destruídos, algumas formigas guerreiras se unem com as formigas engenheiras numa arriscada operação de resgate à rainha. Mas como resgatá-la?
As formigas guias arquitetaram um plano de resgate que consistia em arremessar algumas formigas guerreiras, algumas formigas engenheiras, algumas guias e algumas operárias sobre o formigueiro inimigo. Chegando lá, elas dividiram-se em dois grupos. Um grupo composto pelas formigas guerreiras e formigas guias, incumbira-se de entrar no formigueiro inimigo em busca da rainha. O outro grupo, composto pelas formigas engenheiras e pelas formigas operarias, incumbira-se de fabricar uma catapulta que os arremessasse de volta ao seu formigueiro de origem. Para que nenhum imprevisto ocorresse quando do arremesso da rainha, as formigas engenheiras foram consultadas. Elas então criaram um modelo teórico de catapulta. A catapulta consistia em utilizar um pedaço de matinho de tamanho fixo. A rainha deveria ser colocada em uma ponta, com a catapulta inclinada em um determinado ângulo , e arremessada numa distância exata entre os formigueiros. No entanto, para que isso ocorresse, era necessário saber qual matinho usar. Algumas formigas então começaram a realizar testes com matinho de uma mesma espécie, mas com diferentes diâmetros e verificaram que, para um alcance horizontal fixo igual à distância entre os formigueiros, o ângulo de arremesso variaria com o diâmetro do matinho, segundo a seguinte tabela de dados:
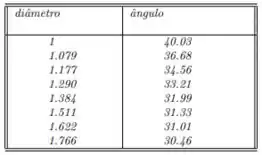
Para encontrar a melhor curva descrita por esses pontos as formigas engenheiras fizeram um programa que encontrava a melhor aproximação pelo método dos mínimos quadrados. Faça você o mesmo que as formigas engenheiras!

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha nessa questão ele deseja encontrar a melhor curva descrita para os pontos da tabela,
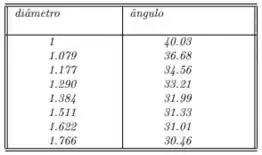
Ficando a média dos diâmetros valendo,
Ficando,
Sendo sua melhor curva descrita a partir do maior ângulo multiplicado pela média,

Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta