Um tubo fino e comprido está imerso na água. Na base do tubo há um reator elétrico, que descreve um movimento sobe-e-desce oscilatório. Em qualquer instante, a coordenada da base do tubo é dada pela fórmula: , onde é a amplitude do movimento e ω é a frequência de oscilação. Medidores de deformação colocados na base do tubo medem a deformação do mesmo, em função da amplitude de oscilação . Os valores da deformação medida em relação as amplitudes encontram-se na tabela:
![]()
Colocando os dados da tabela, num gráfico:
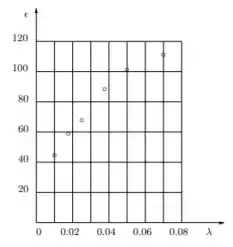
parece apropriado aproximar a função por uma parábola. Assim, usando o método dos mínimos quadrados:
a) ajuste a função por função do tipo: ;
b) Faça um gráfico dos valores de contra , obtidos através da parábola, e marque no mesmo gráfico dos pontos da tabela. Qualitativamente falando, o polinômio é uma boa aproximação?
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide Um tubo fino e comprido está imerso na água. Na base do tubo há um reator elétrico, que descreve um movimento sobe-e-desce oscilatório. Em qualquer instante, a coordenada da base do tubo é dada pela fórmula: , onde é a amplitude do movimento e ω é a frequência de oscilação. Medidores de deformação colocados na base do tubo medem a deformação do mesmo, em função da amplitude de oscilação . Os valores da deformação medida em relação as amplitudes encontram-se na tabela:
![]()
Colocando os dados da tabela, num gráfico:
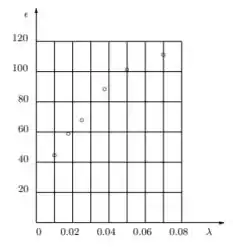
parece apropriado aproximar a função por uma parábola. Assim, usando o método dos mínimos quadrados:
a) ajuste a função por função do tipo: ;
b) Faça um gráfico dos valores de contra , obtidos através da parábola, e marque no mesmo gráfico dos pontos da tabela. Qualitativamente falando, o polinômio é uma boa aproximação?

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha seguindo as variações fornecidas nas tabelas e nos gráficos acima temos que na letra (a) para determinar o ajuste da função;
Temos,
Já para,
Ficando,
Com isso temos que,
Já na letra (b) demonstrando os valores por meio de gráfico temos que,
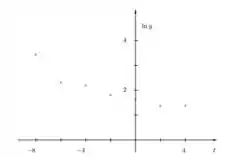

Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a)
b) gráfico demonstrado no passo anterior.