Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 8.Problemas Aplicados e Projetos - Ex. 6

A resistência à compressão do concreto, , decresce com o aumento da razão água/cimento, , (em galões de água por saco de cimento). A resistência à compressão de três amostras de cilindros para várias razões estão mostradas no gráfico a seguir:

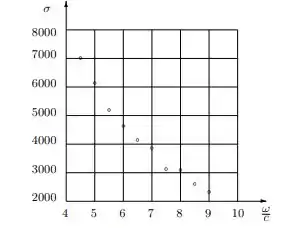
e, cujos valores estão na tabela:

a) Usando o método dos mínimos quadrados, ajuste σ, aos dados, utilizando uma função do tipo:

b) Compare os valores da curva obtida no item a) com os do gráfico, para verificar (por inspeção), se a curva obtida para é uma boa aproximação.

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide dada resistência à compressão do concreto, , decresce com o aumento da razão água/cimento, , (em galões de água por saco de cimento). A resistência à compressão de três amostras de cilindros para várias razões estão mostradas no gráfico a seguir:

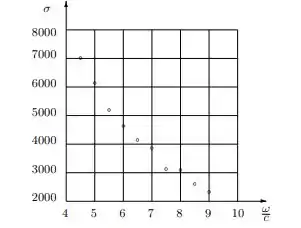
e, cujos valores estão na tabela:

a) Usando o método dos mínimos quadrados, ajuste σ, aos dados, utilizando uma função do tipo:

b) Compare os valores da curva obtida no item a) com os do gráfico, para verificar (por inspeção), se a curva obtida para é uma boa aproximação.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha nessa questão, com base na variação de valores descritos no gráfico e na tabela do passo anterior, temos que na letra (a) para ajustar pelo método dos mínimos quadrados temos que,

Ficando,

Logo temos que que seu formulário seria adotado como,

Já na letra (b) comparando o termo (a) com a curva do gráfico temos que,

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

a) e

Exercícios de Livros Relacionados

Aproximar, pelo método dos mínimos quadrados, a função f ( x )=x 3+4x , no intervalo [ 0,1 ] , a) por uma reta;b) por um polinômio do 2° grau.

Deseja-se aproximar uma função f definida em um intervalo [ a , b ] por uma função g x = x 2 ln ⁡ x 3 a + b x 2 usando o método dos mínimos quadrados.a) Qual é a função a ser minimizada?b) Qual é o si

Ajustar os valores da tabela:através de uma das famílias de funções: a e b x ,1 a + b x ,x a + b x Use o teste de alinhamento para decidir qual das funções melhor resolve o problema.O método dos mínim

Determinar a melhor solução para o sistema:

E possível aproximar diretamente uma função f ( x ) tabelada, por uma função do tipo: g x = a 1 + b cos ⁡ x usando o método dos mínimos quadrados? Se não for possível, qual é a transformação que deve