Área de Superfícies
Produzido por Arthur Melo de AlmeidaTeoria
Introdução
Uma das várias aplicações das integrais de linha, que vamos ver agora, é o cálculo da área de algumas superfícies. A área de qualquer superfície pode ser obtida a partir de uma, pasmem, integral de superfície! Mas existe um caso específico que podemos calcular a área da superfície com uma integral de linha, são as superfícies de revolução.
Superfícies de revolução são superfícies obtidas a partir da rotação de uma curva em torno de algum eixo. Não entendeu? Vê se com esse exemplo fica mais claro! Já estamos familiarizados com a reta , ela é bem simples, né? O que acontece se rodarmos ela em torno do eixo no intervalo ? Olha o esboço como seria:
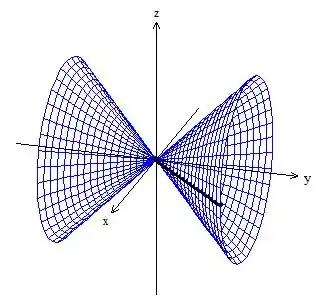
Veja que a linha preta é a nossa curva original . Simplesmente pegamos ela e rodamos em torno do eixo .
Beleza, entendi como é a superfície de rotação, mas e aí? Como calculo sua área? Fica tranquilo, tem um teorema bem simples que vai nos dar a área da superfície de rotação com uma só integral: o Teorema de Pappus
Teorema de Pappus
O Teorema de Pappus diz que, para a rotação de uma curva ao redor do eixo , a área da superfície é dada por:
E para a rotação ao redor do eixo , a área é dada por:
Onde
Temos que tomar alguns cuidados aqui:
1º) A fórmula representa a área de uma rotação completa, por isso o termo ali! Vou te mostrar um exemplo que teríamos que fazer uma modificação nessa fórmula:
Pense na rotação da curva ao redor do eixo no intervalo de . A curva e a superfície vão ser essas aqui:
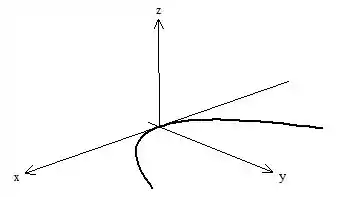
Perceba que, fazendo somente metade da rotação já conseguimos gerar a superfície, né? Isso acontece porque a curva é simétrica em relação ao eixo ! Sempre que tivermos isso vamos ter que pensar em como calcular a área correta. Nesse caso, ao invés de utilizar a fórmula com , vamos simplesmente dividir por dois, afinal nós só fizemos metade da rotação! Sempre esboce suas curvas e superfícies para não calcular a área errada!
2º) Estamos tratando da integral de um módulo, temos que analisar quando o termo é positivo e quando é negativo! Vai ficar mais claro no exemplo a seguir
Exemplo
Vamos tentar calcular a área daquele exemplo lá de cima. Só para relembrar as informações, o exercício rotacionou a curva em torno do eixo no intervalo de
Passo 1: Beleza, o teorema de pappus para a rotação completa no eixo diz isso aqui:
Precisamos primeiro encontrar uma parametrização para a curva, tirar esse módulo de dentro da integral, sem seguida calcular e, por fim, juntar tudo na integral.
Passo 2: Muitas questões vão nos dar a parametrização direto, nesse caso aqui não foi assim. Uma parametrização simples é a seguinte:
Passo 3: Como fazemos pra tirar esse módulo de ai da integral? Precisamos ver quando é positivo e quando é negativo, no nosso caso:
Então precisamos dividir a nossa integral em duas:
Passo 4: Precisamos agora calcular o valor de , pra isso:
Passo 5: Vamos terminar calculando as duas integrais!
Pronto! Bem simples né, aqui vai um breve passo a passo:
Passo 1: Montar o problema, explicitando o teorema de pappus e esclarecendo o que precisa calcular
Passo 2: Obter uma parametrização para a curva.
Passo 3: Retirar o módulo da integral
Passo 4: Calcular
Passo 5: Juntar tudo na integral do teorema de pappus e resolvê-la
Tranquilo, né? Agora é só partir pra alguns exercícios pra garantir que entendemos tudo, vamos lá?