Integral de Superfície - Campo Escalar
Teoria
Fala aí, nós somos o Responde Aí, a maior plataforma de exatas do Brasil e estamos aqui pra salvar o seu semestre hahaha
Hoje vamos bater um papo sobre as integrais de superfície em um campo escalar, preparado? Então bora!!
Conhecimentos Prévios
Bom, antes de você embarcar nessa aventura das integrais de superfície de um campo escalar é interessante você já ter alguns conhecimentos adquiridos. Eu vou deixar eles aqui embaixo listados👇🏾
✅ Parametrização de superfícies - caso explícito
O que é Integral de Superfície?
Uma integral de superfície segue um princípio semelhante ao das integrais duplas. Nas integrais duplas nós pegamos uma função
No caso das integrais de superfície nós não teremos uma função
Representamos uma integral de superfície do seguinte modo:
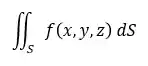
Onde
Como calcular uma Integral de Superfície?
Para calcular uma integral dupla nós vamos usar a seguinte fórmula:
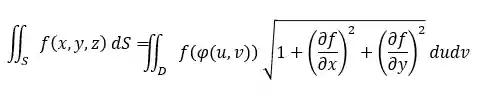
Entendeu nada, né? hahaha. Calma, vamos devagar.
Primeiro vamos entender o que é cada coisa na fómula:
Ainda está meio confuso, não é? Vamos de exemplo para enterder melhor, ok?
Exemplo
Considere a susperfície
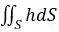
Vamos ir montando juntos um passo a passo para resolução desse problema.
PASSO 1: Parametrizar a superfície
Como a superfície está na sua forma explícita, vamos parametrizá-la como:
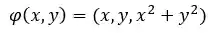
PASSO 2: Achar o domínio de
Para achar o domínio
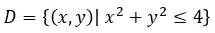
PASSO 3: Calcular as derivadas parciais da função em relação a
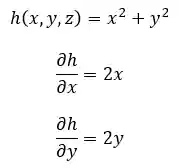
PASSO 4: Escrever a função em termos das variaveis de parametrização.
Nesse caso, como a nossa parametrização foi explícita e as variáveis de parametrização continuam sendo
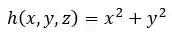
Mas fica atento, porque se a parametrização não for explícita a função muda um pouco quando a escrevemos em termos das variáveis de parametização, beleza?
PASSO 5: Montar a integral.
Vamos pegar a fórmula:
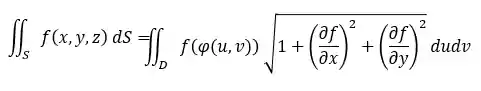
Reescrever em termos de
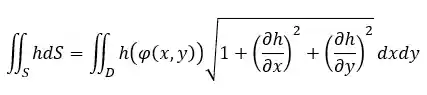
Agora vamos substituir tudo que encontramos até o momento:
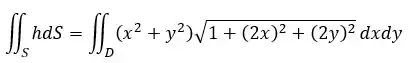
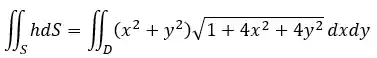
Onde
E agora vamos resolver a integral como resolveríamos uma integral dupla. Nesse caso seria legal usar uma mudança polar (fica a dica 😉).
E é isso que temos para falar pra você sobre as integrais de superfície em um campo escalar. Você pode avançar nos seus estudos e ir entender as integrais de superície em um campo vetorial, conferindo essa nossa página aqui: Integrais de superfície - caso vetorial.
Mas, caso você ainda não esteja seguro para avançar, você pode assistir o vídeo que eu vou deixar aqui em embaixo 👇🏾 sobre integrais de superfície em campo escalar para fixar ainda mais esse conteúdo.
Vídeo
Curtiu nosso conteúdo? Então assina com a gente para ter acesso a muito mais!
O que é Integral de Superfície?
Como calcular uma Integral de Superfície?
Vídeo
Exercícios Resolvidos
Exercício Resolvido #1
Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1153 - 15
Monte, mas não calcule, uma integral iterada à integral de superfície dada projetando no
- Plano
- Plano
- Plano
Onde é a porção do plano no primeiro octante.
Passo 1
a) Calma, é muita informação! Vamos organizar as informações e ver o que ele quer na questão! Primeiro vamos entender a superfície , que é um plano no primeiro octante.
Para desenhar um plano é interessante ver a interseção dele com cada eixo e ligar os pontos:
Para e
Para e
Para z e
Assim a imagem do plano é:
Passo 2
Primeiro vamos fazer a integral projetada no plano , assim, devemos ter somente e variando. Então, devemos substituir e substituir na integral, logo:
Mas quando formos achar a integral iterada à integral de superfície dada projetada em , precisaremos multiplicar o módulo do vetor normal a superfície . Deste modo, vamos fazer a parametrização explicita.
Podemos então fazer a parametrização explícita como abaixo
Como o módulo da normal para a parametrização explícita é:
Como,
Temos que:
Agora podemos montar a integral não esquecendo de multiplicar . Assim a integral fica,
Passo 3
Vamos fazer o mesmo para as outras duas integrais. No plano vamos fazer somente e variando, assim, devemos encontrar e substituir na integral, logo:
A parametrização explícita é dada por
Como o módulo da normal para a parametrização explícita é:
Como,
Temos que:
Assim a integral fica:
Passo 4
Para a última integral. No plano vamos fazer somente e variando, assim, devemos encontrar e substituir na integral, logo:
A parametrização explícita é dada por
Como o módulo da normal para a parametrização explícita é:
Como,
Assim a integral fica:
Passo 5
O próximo passo é encontrar o limites de integração para cada integral. Ou seja, precisamos descobrir o domínio . Mas antes de começar, vamos relembrar aquelas três contas que fizemos para montar o gráfico no Passo 1:
Para e
Para e
Para z e
No plano , temos que o valor de é igual a zero. Logo, para um valor fixo de , vamos avaliar a variação de :
Como estamos tratando do primeiro octante, não pode ser negativo, variando de
Olhando para equações, podemos ver que o valor máximo que pode ter é . Ou seja,
Colocando os limites de integração na integral temos,
No plano , vamos seguir o mesmo raciocínio. Só que agora temos que o valor de é igual a zero. Logo, para um valor fixo de , vamos avaliar a variação de :
Assim,
Colocando os limites de integração na integral temos,
Por fim, no plano , temos que o valor de é igual a zero. Logo, para um valor fixo de , vamos avaliar a variação de :
Assim,
Colocando os limites de integração na integral temos,
Resposta
Assim temos que as integrais são:
Exercício Resolvido #2
Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1154 – 20 - modificado
Monte, mas não calcule, uma integral iterada igual à integral dada
Onde é a porção do cilindro no primeiro octante entre os planos , , e
Passo 1
O primeiro passo é parametrizar a superfície !
Vamos dar uma olhada como é essa superfície e depois parametriza-la.
Primeiro, temos um cilindro circular. Esse círculo tem raio , então vamos ter
Mas ele disse que é limitado pelo plano e , então vamos ter que vai de à só.
Então só vamos pegar a parte do cilindro nessa faixa, que vai ficar
Ele também disse que vai ser limitado pelo planos e , vamos desenhar esses planos aqui
Então a nossa superfície vai ser o cilindro vermelho limitado entre esses planos azuis.
Passo 2
Vamos para a parametrização desse cilindro
Podemos parametrizar a superfície com coordenadas cilíndricas. Segue que:
Aplicando na equação do cilindro:
Portanto, o parâmetro sumiu. Até agora temos que a nossa parametrização é:
Ou seja, como é uma superfície precisamos necessariamente de dois parâmetros. Como um deles sumiu, inventamos um outro qualquer . Como se trata de um cilindro, podemos deixar o sendo o próprio parâmetro :
Logo:
E está parametrizado.
Passo 3
Agora precisamos dos limites desses parâmetros.
O enunciado nos fala que ele quer “a parte do cilindro no primeiro octante”, certo? Isso nos dá o intervalo de
Passo 4
Agora precisamos achar o intervalo de .
Repara que , então o vai estar limitado pelos planos e , ou seja,
Mas como :
Só que , então temos que:
E agora temos os dois limites da nossa parametrização, ela vai ser
Com
Passo 5
Agora que temos a parametrização, precisamos fazer a nossa integral de superfície.
Para isso precisamos achar o vetor normal , para depois pegar o módulo dele.
Lembra como faz?
Vamos fazer o nosso produto vetorial
Vamos achar essas derivadas parciais primeiro, lembrando que nossa parametrização é
Então nossas derivadas parciais são:
E
Então nosso vetor normal vai ser:
Passo 6
O módulo disso vai ficar
Passo 7
A nossa integral vai ser
Vamos trocar e pelos seus valores da parametrização
Vamos ter
Como a questão não pede pra gente resolver a integral, a resposta é isso aí =D
Resposta
Exercício Resolvido #3
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 261-4b.
Calcule a área da superfície do cone situada entre os planos e .
Passo 1
Começamos com a parametrização da superfície em questão. Como se trata de um cone, é razoável utilizar coordenadas esféricas ou cilíndricas. Entretanto, uma coisa que devemos sempre prestar atenção é nas equações das superfícies que limitam a que queremos descobrir a área.
Como se tratam de planos, não é adequada nenhuma parametrização que envolva funções trigonométricas (i.e. cilíndrica e esférica). Portanto, a melhor parametrização que conseguimos obter é a explícita...
Encontrando em função de e obtemos:
Podemos perceber que são duas parametrizações possíveis. Afinal de contas o cone tem uma parte superior e uma inferior. Como estamos integrando entre e um outro plano, podemos observar pelos cortes desses planos que só precisamos parametrizar a parte superior do cone.
Se você não tiver a intuição de qual corte fazer, tente todos os três possíveis: , , . Basta em cada um igualar uma das variáveis à uma constante (geralmente zero).
No plano , que é o plano , temos essa revelação. Neste plano o corte do cone é:
Representado em laranja. Ao passo que o corte do plano:
É representado em azul.
Portanto:
Passo 2
Vamos determinar agora as limitações da superfície em termos da nossa parametrização:
Agora vamos ver como é que o outro plano encontra com o nosso cone:
Substituindo na equação do cone:
Completando o quadrado perfeito:
Como chegamos à esse negócio mesmo? Ah sim, nós igualamos a equação do plano à do cone. Então nós conseguimos encontrar a equação dos pontos que pertencem tanto à um quanto ao outro. Por consequência, a região dos pontos do cone que estão entre um plano e outro é dos pontos que estão no interior desta elipse:
Ou seja, nossa parametrização é:
Ao passo que nosso domínio é:
Dá pra ver que não vai dar muito certo fazer essa conta aí por causa do domínio... Mais tarde voltaremos nisso.
Passo 3
Para aplicar a fórmula da área precisamos do módulo do vetor normal:
Calculando as derivadas parciais:
Fazendo o produto vetorial:
E calculamos o módulo:
Passo 4
Aplicando a fórmula, temos:
Sendo que:
O detalhe é que fazer essa conta obviamente não vai ser agradável... Vamos trocar de coordenadas por favor? Implementando coordenadas polares, obtemos:
Daí tiramos que nosso domínio vai ser:
Falta só calcular o Jacobiano para trocar de variáveis. Lembrando lá das mudanças polares
Substituindo na integral os limites de integração junto com o jacobiano:
Como são independentes nos limites de integração as variáveis e , separamos as integrais:
Finalmente encerramos!
Resposta
Exercício Resolvido #4
UNICAMP - Cálculo 2 - P3 2014 Tarde – 3
Determine a área da parte do paraboloide hiperbólico que se encontra entre os cilindros e .
Passo 1
Vamos começar desenhando essa região. Temos um parabolóide (sela) cortado por dois cilindros centrados na origem, com raios e .:
O problema nos pede então a área da parte do paraboloide que está entre os dois cilindros. Vendo de cima, temos isso aqui:
Beleza, vamos usar essa fórmula aqui para calcular a área da superfície:
Passo 2
Agora precisamos parametrizar a superfície. Como nossa equação é , vamos usar e como parâmetros, ok? Temos então:
Onde e se encontram entre as circunferências verde e azul que desenhamos no passo anterior, a projeção da nossa superfíce cortada no plano .
Passo 3
Calcular e
Passo 4
Calcular
Passo 5
Agora vamos montar a integral
Onde é a região entre as circunferências:
Que são os cilindros e vistos de cima. Bom, vamos usar coordenadas polares então, né?
Isso nos dá
Como a região completa uma volta no plano , temos . O raio vai desde a circunferência azul até a verde, portanto, . Susbstituindo na integral, temos:
Passo 6
Agora vamos resolver essa integral aí. Vamos fazer a substituição:
Resposta
Exercício Resolvido #5
USP - Cálculo 3 - P3 2013 - 1ª
Determine a massa da superfície dada por limitada por , sabendo que a densidade é dada por .
Passo 1
Para acharmos a massa, temos que fazer a integral de superfície da densidade, ou seja, vai ser uma parada assim
Como temos escrito bonitinho em função de e podemos parametrizar essa curva como
Precisamos achar o valor de nessa bagunça, repara que temos
Então
Então teremos
Passo 2
Temos uma integral de superfície escalar, então precisamos achar a norma do vetor normal, primeiro vamos achar o vetor normal, ele vai ser
Vamos começar achando as derivadas da parametrização
O vetor normal vai ser
Passo 3
A norma vai ficar
Passo 4
A integral vai ficar
Onde é
Vamos ter
Passo 5
Temos uma integral que a região sai facin por coordenadas polares, então vamos fazer
Com e
Passo 6
A integral vai ficar
Lembrando que
E
Vamos ter
Resposta
Exercício Resolvido #6
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 261-4e.
Calcule a área da parte superior da esfera contida no interior do cilindro .
Passo 1
Antes de mais nada, temos que parametrizar nossa superfície. Como se trata de uma esfera, nada melhor que coordenadas esféricas, de forma que, como já sabemos, a parametrização fica:
Como temos que o raio é , a parametrização de fato fica:
Passo 2
Agora temos que limitar a nossa região de integração. Sabemos que a esfera está no interior do cilindro:
Apesar de que não sabemos como desenhar essa forma bizarra, o fato é que já temos uma parametrização para e , portanto podemos substituí-la para ver se ajuda na nossa análise. Nós chegamos anteriormente que:
Repare: Ao substituirmos a nossa parametrização da esfera na equação do cilindro, estamos averiguando os valores de e de para os quais a esfera e o cilindro são iguais, ou seja, onde os gráficos se encontram, e não onde na esfera estamos dentro do cilindro (que é o que o enunciado pede).
Substituindo:
Arrumando:
Utilizando a relação de soma de arcos:
Não podemos dividir ambos os lados por pois esse valor pode ser igual à zero, dependendo de . Vamos então tentar resolver:
Pronto. Os nossos limites de integração tem que sair da análise que vamos fazer da equação acima.
Passo 3
Como a esfera encontra com o cilindro quando essa equação acima é satisfeita, ela encontra quando ou quando .
Como sabemos que o ângulo , por definição, pertence ao intervalo , sabemos que o seu seno não pode assumir valores negativos como . Logo, é razoável assumir que os pontos da esfera que estão dentro do cilindro respeitam esta relação:
E o ? Como fica? Normalmente deixamos ele assumir qualquer valor, mas vamos ver se isto é valido neste caso. Olhando a equação abaixo percebemos uma coisa peculiar:
As duas variáveis são independentes. O que significa que o pode assumir valores diferentes de zero, independentemente do . Portanto, se tivermos:
Podemos dividir ambos os lados da equação por que não tem problema. Neste caso, observamos:
Ou seja, aqui fica mais claro uma coisa com relação à . O lado esquerdo da equação acima é um quadrado perfeito, portanto sempre positivo. Ao passo que o lado direito poderia assumir valores negativos. Não podemos deixar isto acontecer, para que a equação tenha sentido. Portanto:
Como estipulamos que está no intervalo , portanto está em , logo os valores que satisfazem esta equação neste intervalo são:
Dividindo por dois as inequações, temos que o intervalo ao qual pertence é:
Portanto, o nosso domínio de integração vai ser:
Passo 4
Aplicando a fórmula da integral de superfície:
Já sabemos quanto dá esse vetor normal da esfera, mas por prática nós vamos calcular tudo, começando pelas derivadas parciais:
Calculando o produto vetorial:
Fica uma dica aqui: você pode fatorar do determinante do produto vetorial um termo de uma linha ou coluna dele. No caso nunca vamos fatorar as colunas porque o primeiro elemento é sempre um vetor (), mas de resto esse truque é bastante útil. Na última linha podemos fatorar o :
Pra quem acha que vai ajudar também pode fatorar da segunda linha o , lembrando que vai sobrar na última coluna. Eu não acho tão útil assim porque pode confundir mais depois, mas fica à critério de cada um. Seguindo:
Fazendo a distributiva do que nós pusemos em evidência lá em cima:
Passo 5
Buscando o módulo dessa monstruosidade:
It’s Algebra Time, baby! Pondo em evidência:
Pondo em evidência:
Como o ângulo , por definição, pertence ao intervalo ele nunca é negativo, portanto:
Passo 6
Finalmente, podemos plugar os valores dos limites de integração na fórmula. Lembrando que os valores de se encontram numa união de intervalos, então teríamos que fazer quatro integrais (que vão dar a mesma coisa no final...). Aproveitando a simetria do problema, podemos simplesmente usar apenas um intervalo e multiplicar a integral por quatro. Plugando:
Integrando o seno obtemos:
Aplicando com os valores de integração:
Essa bagunça de cosseno do arco seno pode ser resolvida da seguinte maneira. Forçando a existência de um triângulo de hipotenusa e cateto oposto igual à :
O ângulo é o arco cujo seno é , logo ele é . O que queremos é o seu cosseno:
Plugando na outra integral:
Arrumando essa raiz de cosseno de :
Plugando na expressão problemática:
Cuidado quando for tirar o seno ao quadrado da raiz, pois ele poderia admitir valores negativos, portanto tem que ser o módulo:
Felizmente no intervalo que estamos integrando o seno é sempre positivo. Logo:
Prosseguindo:
Depois dessa Odisseia, encerramos a questão. É isso aí meu amigo. Valar Calculis: Todos os Cálculos tem que morrer!