Exercícios de Integral de Superfície de Função Escalar - Lista de Exercícios Resolvida
Questão 1
Determine a massa da superfície dada por limitada por , sabendo que a densidade é dada por .
Ver solução completaQuestão 2
Calcule a área da parte superior da esfera contida no interior do cilindro .
Ver solução completaQuestão 3
Monte, mas não calcule, uma integral iterada à integral de superfície dada projetando no
- Plano
- Plano
- Plano
Onde é a porção do plano no primeiro octante.
Ver solução completaQuestão 4
Determine a área da parte do paraboloide hiperbólico que se encontra entre os cilindros e .
Ver solução completaQuestão 6
Monte, mas não calcule, uma integral iterada igual à integral dada
Onde é a porção do cilindro no primeiro octante entre os planos , , e
Ver solução completaQuestão 8
Calcule a integral de superfície , onde é a parte do elipsóide contida no semi-espaço .
Ver solução completaQuestão 10
Encontre a área da superfície que está acima do triângulo com vértices , e .
Ver solução completaQuestão 11
Calcule a área da superfície S do semicone
Contida no interior do elipsoide:
Ver solução completaQuestão 12
Calcule a integral de superfície escalar:
Sendo a porção do cilindro:
Contida no primeiro octante, limitada superiormente por:
E inferiormente por:
Ver solução completaQuestão 13
Considere a superfície do paraboloide , situada no primeiro octante .
- Ache uma parametrização para .
- Calcule a área de .
Questão 14
Calcule a integral de superfície
é a parte do plano que está no primeiro octante.
Ver solução completaQuestão 15
Nos exercícios 16 -> 25, calcule
onde é a parte do paraboloide que está situada acima do plano .
Ver solução completaQuestão 16
Dada a função , é correto afirmar:
- para C dado por
- f é analítica
- para o caminho fechado C.
Questão 18
Calcule a integral de superfície abaixo
Onde é a porção do cone acima do plano e limitada entre os planos e .
Ver solução completaQuestão 19
Sobre a seria complexa é correto afirmar:
- A serie converge se .
- A serie converge se .
- A serie não converge absolutamente para nenhum ponto.
- A soma da série é
- A serie diverge se
Questão 20
Sobre os números complexos é correto afirmar:
- Se e então
- É um conjunto comutativo com relação à adição e à multiplicação.
- Todo numero complexo possui um inverso
- Todo numero complexo possui pelo menos uma raiz quadrada
- Todo número complexo possui um conjugado
Questão 21
Calcule a integral de superfície
onde S é o limite da região delimitada pelo cilindro e pelos planos e .
Ver solução completaQuestão 22
Justifique se as seguintes afirmações são verdadeiras ou falsas.
- O campo vetorial
- A área da parte superior que está dentro do cilindro , é .
é um campo vetorial conservativo com função potencial .
Questão 23
Calcule a massa da superfície onde , com densidade pontual de massa .
Ver solução completaQuestão 24
Determine a área da parte do paraboloide hiperbólico que está entre os cilindros e
Ver solução completaQuestão 25
14) Seja a porção da esfera que se encontra dentro do paraboloide
Calcule a massa de sabendo que a densidade de massa em cada ponto é igual ao quadrado da distância do ponto ao eixo .
Ver solução completaQuestão 26
13) Seja a superfície do sólido limitado inferiormente pelo paraboloide e superiormente pelo plano . Se a densidade de massa é dada por , calcule a massa de .
Ver solução completaQuestão 27
Seja a superfície de rotação obtida girando em torno do eixo . Calcule a massa de , sabendo que a densidade em cada ponto é proporcional à distância do ponto ao eixo .
Ver solução completaQuestão 28
4) Calcule a área das superfícies:
g) parte da superfície , compreendida entre os planos , , e .
Ver solução completaQuestão 29
4) Calcule a área das superfícies:
a) porção do plano , que está dentro do cilindro .
Ver solução completaQuestão 31
4) Calcule a área das superfícies:
f) superfície gerada pela rotação do segmento de reta , , em torno do eixo .
Ver solução completaQuestão 32
11) Calcule a massa da superfície parte do plano dentro do cilindro , sendo a densidade dada por .
Ver solução completaQuestão 33
4) Calcule a área das superfícies:
e) superfície gerada pela rotação do conjunto em torno do eixo .
Ver solução completaQuestão 34
Deseja-se construir uma peça de zinco que tem a forma da superfície de equação , compreendida entre os planos e e o cilindro . Se o metro quadrado do zinco custa reais, calcule o preço total da peça.
Ver solução completaQuestão 35
9) Calcule
Onde
e) e é a porção do cilindro , , no primeiro octante, entre os planos e .
Ver solução completaQuestão 37
12) Seja a porção do cilindro , com , limitada pelo plano e pelo plano . Calcule a massa de , sabendo que a densidade de massa em um ponto é igual ao quadrado da distância do ponto ao eixo .
Ver solução completaQuestão 39
13) Seja a superfície do sólido limitado inferiormente pelo paraboloide e superiormente pelo plano . Se a densidade de massa é dada por , calcule a massa de .
Ver solução completaQuestão 40
Seja S a superfície definida pela parte do plano que está dentro do cilindro .
- Determine uma parametrização para a superfície S juntamente com o domínio D da parametrização.
- Parametrize o bordo da superfície.
- Use a parametrização para explicitar o elemento de área de superfície.
- Calcule a integral
Questão 41
Considere o cone .
a) Calcule a área da parte da superfície que se encontra no primeiro octante (ou seja, , , ) e abaixo do plano .
Ver solução completaQuestão 42
Calcule a integral de superfície
onde S é a parte do cilindro que esta entre os planos x=0 e x=3 no primeiro octante.
Ver solução completaQuestão 43
Seja a esfera de equação com densidade superficial . A massa de é igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 45
Considere a superfície parametrizada
Cuja imagem denotaremos por .
- Calcule uma equação implícita para .
- Faça um esboço de .
- É uma superfície parametrizada regular ou não? Justifique a resposta.
- Calcule a equação implícita do plano tangente a no ponto
- Calcule a integral de superfície
Questão 46
Considere a superfície parametrizada por
Com e
(a) Determine o vetor normal unitário de no ponto de que aponta para cima
(b) Calcule a área de .
Ver solução completaQuestão 48
Considere a parte do cilindro que fica na intersecção das regiões , e .
- Determine uma parametrização de , especificando o domínio de definição da parametrização.
- Calcule a integral de superfície .
Questão 49
Considere a parte da superfície que fica embaixo da superfície , isto é,
- Determine uma parametrização de , especificando o domínio de definição da parametrização.
- Calcule a área da superfície .
Questão 51
Questão :
a) Seja a parte do cilindro que está no interior do cilindro com . Calcule a massa de sendo a densidade .
Ver solução completaQuestão 52
Questão 3) Calcule a área da parte do paraboloide elíptico que se encontra dentro do cilindro .
Ver solução completaQuestão 53
Questão 2) Calcule a integral de superfície
onde é a parte do plano que está no primeiro octante.
Ver solução completaQuestão 54
Questão 1) Seja a superfície da esfera que está dentro do cone
- Esboce a superfície .
- Parametrize a superfície.
- Determine o vetor unitário no ponto que aponta para baixo.
- Calcule a área de .
Questão 55
Questão 4: Considere o corpo sólido no interior do cilindro , limitado por cima e por baixo pelo cone . Calcule a área de superfície de .
Sugestão: Evite a parametrização do cilindro como superfície de revolução com eixo deslocado!
Ver solução completaQuestão 56
Questão 1: Seja a superfície parametrizada
- Faça um esboço da imagem de .
- Justifique se a imagem de é uma superfície regular ou não.
- Calcule a equação implícita do plano tangente em .
- Calcule
Questão 57
Seja S a parte da superfície de equação acima do triangulo de vértices (0,0), (1,1), (0,1).
(2.1) Encontre uma parametrização para S e determine o elemento de superfície dS de S. Explicite o domínio da parametrização em termos das coordenadas.
(2.2)Calcule a integral de superfície.
Ver solução completaQuestão 59
4) Calcule a área das superfícies:
h) parte do cone , que se encontra dentro do cilindro , fora do cilindro .
Ver solução completaQuestão 60
Calcule a área da superfície da esfera de raio , centrada na origem, limitada por dois paralelos e dois meridianos, sabendo que o ângulo entre os meridianos é e a distância entre os planos que contêm os paralelos é .
Ver solução completaQuestão 61
Suponha que , onde é a função de uma variável, tal que . Calcule , onde é a esfera
Ver solução completaQuestão 62
Observe a figura abaixo que representa o toro obtido girando em torno do eixo uma circunferência com centro no ponto e com raio . A distância do ponto à origem é .
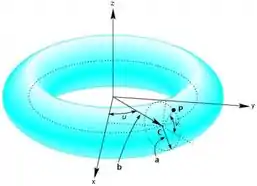
- Mostre que , é a representação paramétrica do toro, onde
- Calcule o vetor normal ao toro no ponto
- Calcule a área do toro
Questão 63
Seja a superfície obtida pela rotação da curva em torno do eixo . Seja , onde , uma parametrização de . Considere a função escalar .
- Calcule
- Encontre a equação do plano tangente que passa pelo ponto correspondente a
- Calcule
Questão 64
Calcule a massa das superfícies sendo a densidade pontual de massa para:
é o triângulo com vértices e e .
Ver solução completaQuestão 65
Calcule a área da superfície da equação compreendida entre os planos , , e o cilindro .
Ver solução completaQuestão 66
1. Calcule a integral de superfície:
d) , é a parte do cilindro , entre os planos e .
Ver solução completaQuestão 68
1. Calcule a integral de superfície:
b) , é a parte do cone que está entre os planos e .
Ver solução completaQuestão 69
(Cap. 16.7 – Exercício 20) Calcule a integral de superfície.
é a parte do cilindro entre os planos e , juntamente com os discos inferior e superior.
Ver solução completaQuestão 70
(6) Considere , e tais que . A área da parte da superfície , , que fica dentro do cilindro é:
Questão 71
(Capítulo 15.6 – Exercício 1) Determine a área da superfície.
A parte do plano que está acima do retângulo .
Ver solução completaQuestão 72
Determine as equações paramétricas e a área da superfície obtida pela rotação da função , em torno do eixo .
(Não precisa resolver a integral)
Ver solução completaQuestão 74
(Cap.16.7- Exercício 9) Calcule a integral de superfície.
S é a parte do plano que está acima do retângulo
Ver solução completaQuestão 75
(Cap.16.7 - Exercício 8) Calcule a integral de superfície.
S é a superfície com equação vetorial.
Ver solução completaQuestão 76
(Cap. 16.7 - Exercício 13) Calcule a integral de superfície.
é a parte do cone que está entre os planos e
Ver solução completaQuestão 77
(Cap. 16.7 - Exercício 5) Calcule a integral de superfície.
S é o paralelogramo com equações paramétricas ,
Ver solução completaQuestão 78
(Cap. 16.7- Exercício 16) Calcule a integral de superfície.
é a parte da esfera que está dentro do cilindro e acima do plano .
Ver solução completaQuestão 79
(Cap.16.7 - Exercício 7) Calcule a integral de superfície.
S é o helicoide com equação vetorial
Ver solução completaQuestão 80
(Cap. 16.7 - Exercício 10) Calcule a integral de superfície.
S é a parte do plano que está no primeiro octante.
Ver solução completaQuestão 81
(Cap 16.7 - Exercício 17) Calcule a integral de superfície.
é o hemisfério
Ver solução completaQuestão 82
(Cap 16.7- Exercício 18) Calcule a integral de superfície.
é o limite da região delimitada pelo cilindro e pelos planos e
Ver solução completaQuestão 83
Calcule as seguintes integrais de superfícies:
onde é a superfície dada por ;
Ver solução completaQuestão 85
Calcule as seguintes integrais de superfícies:
onde é o hemisfério , ;
Ver solução completaQuestão 86
Calcule as seguintes integrais de superfícies:
onde é a parte do plano limitada pelo cilindro
Ver solução completaQuestão 88
Calcule a massa das superfícies sendo a densidade pontual de massa para:
é a parte do plano contida no primeiro octante e .
Ver solução completaQuestão 89
Calcule as seguintes integrais de superfícies:
onde é a parte de limitada por .
Ver solução completaQuestão 90
Calcule a massa das superfícies sendo a densidade pontual de massa para:
é a parte do paraboloide contida no semiespaço e .
Ver solução completaQuestão 91
Calcule a massa das superfícies sendo a densidade pontual de massa para:
é a parte de limitada pelos cilindros e e .
Ver solução completaQuestão 93
6) Seja a superfície de equação , , . Sabendo-se que a área de vale , determine o valor de .
Ver solução completaQuestão 94
Questão 1: Considere a parte do paraboloide hiperbólico onde .
- Determine uma parametrização da superfície , especificando o domínio de definição.
- Usando a parametrização, calcule a integral de superfície da função escalar
Questão 95
Questão 6. Calcule as seguintes integrais de superfícies.
(a) , é a parte do plano que está abaixo do retângulo ;
Ver solução completaQuestão 96
9) Calcule , onde
d) e é a superfície do sólido limitado pelo cilindro e os planos e .
Ver solução completaQuestão 98
8) O cilindro divide a esfera em duas regiões e , onde está no interior do cilindro e fora. Ache a razão das áreas .
Ver solução completaQuestão 99
Determine a área da parte do paraboloide hiperbólico que se encontra entre os cilindros e .
Ver solução completaQuestão 100
Calcule as seguintes integrais de superfícies:
onde S o bordo da região limitada pelo cilindro e pelos planos e ;
Ver solução completaQuestão 101
Calcule as seguintes integrais de superfícies:
onde S e a parte de com 1 ≤ z ≤ 3;
Ver solução completaQuestão 103
Seja o pedaço do cone acima do cilindro e embaixo do cilindro . Calcule a área da superfície S.
Ver solução completaQuestão 104
4) Calcule a área das superfícies:
c) porção do cilindro , entre os planos e .
Ver solução completaQuestão 105
Determine a área da lâmina do cilindro circular em contida entre o plano e o cilindro parabólico , no primeiro octante.
Ver solução completaQuestão 106
Observe a figura abaixo, a região hachurada é limitada pelas curvas e .
Escreva às integrais duplas necessárias para encontrar a área da região hachurada. Detalhe os pedaços de regiões utilizadas na sua decomposição.
Não é necessário calcular as integrais.
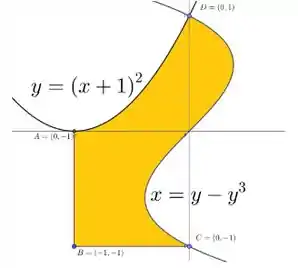
Questão 107
Observe a figura abaixo, a região hachurada é limitada pelas curvas e .
Escreva às integrais duplas necessárias para encontrar a área da região hachurada. Detalhe os pedaços de regiões utilizadas na sua decomposição.
Não é necessário calcular as integrais.
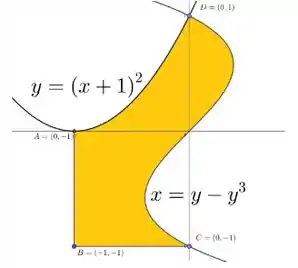
Questão 109
Seja a superfície parametrizada por:
Calcule a integral de superfície:
Ver solução completaQuestão 110
Seja a superfície do cilindro com , e contida no semi espaço . Calcule a área de .
Ver solução completaQuestão 111
( Cap. 16.7- Exercício 19) Calcule a integral de superfície.
é a parte do cilindro que está entre os planos e no primeiro octante
Ver solução completaQuestão 112
Avalie a integral da superfície , onde o campo vetorial F é definido por , e S é a superfície de tetraedro com vértices (0,0,0), (1,0,0), (0,1,0) e (0,0,1).
Ver solução completaQuestão 113
9) Calcule
Onde
e) e é a parte da superfície cônica , limitada por , com .
Ver solução completaQuestão 114
9) Calcule
Onde
e) e é a porção da esfera , limitada pelos planos e .
Ver solução completaQuestão 115
6) Calcule o fluxo do campo , através da superfície do sólido limitado pelo cilindro e pelos planos e , com a normal apontando para fora do sólido.
Ver solução completaQuestão 116
Seja a parte da superfície com e , limitada pelos planos e . Então, o valor de é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 117
Questão 1: Seja a superfície parametrizada
- Calcule a equação cartesiana da imagem de.
- Faça um esboço da imagem de .
- Justifique se a imagem de é uma superfície regular ou não.
- Calcule a equação implícita do plano tangente no ponto
- Calcule
Questão 118
Considere a superfície .
- Esboce a superfície .
- Parametrize a superfície .
- Determine o vetor normal unitário no ponto que aponta para cima.
- Calcule a área de .
Questão 120
Calcule a integral de superfície.
é a parte da esfera que está dentro do cilindro e acima do plano .
Ver solução completaQuestão 121
Avalie a integral de superfície para o campo vetorial dado e a superfície orientada . Em outras palavras, localize o fluxo de através de. Para superfícies fechadas, use a orientação (para o exterior) positiva.
Ver solução completaQuestão 122
Calcule a integral de superfície para o campo vetorial e superfície orientada . Em outras palavras, determine o fluxo de através de . Para superfícies fechadas, use a orientação positiva (para fora).
é a superfície com orientação para cima.
Ver solução completaQuestão 123
Calcule as seguintes integrais de superfícies.
d) , S é a semiesfera
Ver solução completaQuestão 124
Calcule a integral de superfície
Onde é a parte do parabolóide hiperbólico dentro do parabolóide .
Ver solução completaQuestão 125
Calcule
- é a fronteira da região limitada pelas curvas e com orientada no sentido horário.
- , onde é a curva percorrida do ponto
- , onde é a circunferência orientada no sentido horário
- , onde é a fronteira da , no sentido horário.
Questão 126
A integral de linha do campo sobre a curva dada pela intersecção do plano com o parabolóide , orientada de modo que sua projeção no plano é percorrida no sentido anti-horário é
Ver solução completaQuestão 127
Analise as seguintes afirmações sobre o campo :
.
é conservativo em seu domínio.
A integral de superfície de sobre qualquer esfera de raio é .
Podemos afirmar que
todas as afirmações são verdadeiras.
apenas as afirmações e são verdadeiras.
apenas as afirmações e são verdadeiras.
apenas a afirmação é verdadeira.
apenas a afirmação é verdadeira.
Ver solução completaQuestão 128
Considere o campo . O trabalho realizado para deslocar uma partícula ao longo de uma curva lisa e simples contida na esfera com ponto inicial e ponto final é
Ver solução completaQuestão 129
Seja uma curva plana simples, fechada e lisa por partes, percorrida uma vez no sentido horário. Dê todos os valores possíveis para
Questão 130
Calcule a integral de superfície.
é o paralelogramo com as equações paramétricas .
Ver solução completaQuestão 131
Avalie a integral de superfície para o campo vetorial dado e a superfície orientada . Em outras palavras, localize o fluxo de através de. Para superfícies fechadas, use a orientação (para o exterior) positiva.
Ver solução completaQuestão 132
4) Calcule a área das Superfícies:
b) Parte da esfera , interior ao cone
Ver solução completaQuestão 133
4) Calcule a área das superfícies:
d) parte do cilindro , limitado pelo plano e o .
Ver solução completaQuestão 134
Nos exercícios , calcule a área da superfície .
08. é a superfície do paraboloide , situada abaixo do plano .
Ver solução completaQuestão 135
Nos exercícios , calcule a área da superfície .
07. é a superfície do cone interna ao cilindro circular .
Ver solução completaQuestão 136
Nos exercícios , calcule a área da superfície .
06. é a superfície de uma esfera de raio .
Ver solução completaQuestão 137
Nos exercícios , calcule a área da superfície .
10. é a porção do plano que está no primeiro octante.
Ver solução completaQuestão 138
Nos exercícios , calcule a área da superfície .
11. é a superfície do cilindro , cortada pelos planos , e .
Ver solução completaQuestão 139
Nos exercícios , calcule a área da superfície .
12. é a parte da esfera , interna ao cone .
Ver solução completaQuestão 140
Nos exercícios , calcule a área da superfície .
13. é a superfície plana de fronteira triangular com vértices em e .
Ver solução completaQuestão 141
Nos exercícios , calcule a área da superfície .
15. é a superfície correspondente à porção do cilindro circular com altura .
Ver solução completaQuestão 142
Nos exercícios , calcule a área da superfície .
05. é a superfície representada por , para e .
Ver solução completaQuestão 143
Nos exercícios , calcule a área da superfície .
09. é a parte da superfície descrita por , situada acima da região circular .
Ver solução completaQuestão 144
Nos exercícios , calcule a área da superfície .
14. é dada pela equação e se encontra sobre a região .
Ver solução completaQuestão 145
Calcule
- a elipse , percorrida de com
- sendo a circunferência percorrida de a com .
- sendo a fronteira do retângulo e , percorrida no sentido anti-horário.
Questão 146
Calcule
- é a fronteira da região limitada pelas curvas e com orientada no sentido horário.
- , onde é a curva percorrida do ponto
- , onde é a circunferência orientada no sentido horário
- , onde é a fronteira da , no sentido horário.
Questão 147
Um campo de vetores em se diz radial (ou central) se existe uma função tal que onde Suponha que é de classe . Mostre que é conservativo.
Ver solução completaQuestão 149
Suponha:
- Uma superfície S dada por
- é a intersecção de S com
- é a intersecção de S com
Escolha um dos campos vetoriais para a partir de S, γ1 e γ2 elaborar:
i. um exercício que envolva o cálculo de Trabalho.
Ver solução completaQuestão 151
Nos exercícios 16 -> 25, calcule
onde é a porção do plano interior ao cilindro .
Ver solução completaQuestão 153
Nos exercícios 16 -> 25, calcule
onde é a porção do cilindro , compreendida entre os planos e
Ver solução completaQuestão 154
Nos exercícios 16 -> 25, calcule
onde é a parte da esfera situada entre os planos e
Ver solução completaQuestão 155
Nos exercícios 16 -> 25, calcule
onde a parte do plano contida no cilindro .
Ver solução completaQuestão 156
Forneça o resultado numérico da parte imaginaria da integral sendo o caminho C dado pela parametrização ,
Ver solução completaQuestão 157
Suponha:
- Uma superfície S dada por
- é a intersecção de S com
- é a intersecção de S com
Escolha um dos campos vetoriais para a partir de S, γ1 e γ2 elaborar:
ii. um exercício que envolva o cálculo de Fluxo.
Ver solução completaQuestão 158
Calcule a massa das superfícies sendo a densidade pontual de massa para:
é a parte de limitada por e
Ver solução completa