Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 52

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.

A Parte da superfície z = c o s ⁡ ( x 2 + y 2 ) que está dentro do cilindro x 2 + y 2 = 1 .

Passo 1

E ai turma, beleza?

Nosso objetivo nessa questão é encontrar a área da superfície com uma precisão de quatro casa decimais.

A superfície é:

z = c o s ⁡ ( x 2 + y 2 )

Que está dentro do cilindro:

x 2 + y 2 = 1

Vamos ter que lembrar de algumas formulas, beleza!!?

Quando temos uma função do tipo z = f ( x , y ) a área de superfície pode ser expressa como:

A = ∬ 1 + f x 2 + f y 2 d A

Onde f x e f y são as derivadas em relação a x e y . Até ai tudo bem né pessoal!

Quem é nossa região de integração d A ? Repare que ele disse que está dentro do cilindro de raio 1 :

x 2 + y 2 = 1

Aqui, podemos utilizar coordenadas polares. E como é um cilindro completo, vamos ter:

x = r cos ⁡ θ

y = r   s e n   θ

d A = r d r d θ

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π  

Para estimar o valor da integral, você pode utilizar uma calculadora de integrais de sua preferência. Aqui vamos utilizar a WolframAlpha.

Agora ficou moleza ein! Vamos nesssa!

Passo 2

Vamos começar calculando as derivadas em relação a x e y da função:

z = f x , y = c o s ⁡ ( x 2 + y 2 )

Derivando em relação a x , vamos ter:

∂ z ∂ x = ∂ ∂ x cos ⁡ x 2 + y 2 = - 2 x s e n   ( x 2 + y 2 )

Derivando em relação a y , temos:

∂ z ∂ y = ∂ ∂ y cos ⁡ x 2 + y 2 = - 2 y s e n   ( x 2 + y 2 )

Substituindo na integral:

A = ∬ 1 + f x 2 + f y 2 d A

Vamos ter:

A = ∬ 1 + ( - 2 x s e n x 2 + y 2 ) 2 + ( - 2 y s e n x 2 + y 2 ) 2 d A

A = ∬ 1 + 4 x 2 s e n 2 x 2 + y 2 + 4 y 2 s e n 2 x 2 + y 2 d A

Assim a área A fica:

A = ∬ 1 + 4 ( x 2 + y 2 ) . s e n 2 x 2 + y 2 d A

Passo 3

Agora, para resolver essa integral vamos mudar para coordenadas polares. Assim:

x = r cos ⁡ θ

y = r   s e n   θ

d A = r d r d θ

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π  

Substituindo na integral, em coordenadas polares ficará:

A = ∫ 0 2 π ∫ 0 1 1 + 4 r 2 s e n 2 r 2   r d r d θ

Repare que nenhum termo depende de θ , assim podemos integrar em d θ primeiro.

A = ∫ 0 2 π d θ ∫ 0 1 1 + 4 r 2 s e n 2 r 2   r d r

Ficando com:

A = 2 π ∫ 0 1 r 1 + 4 r 2 s e n 2 r 2   d r

Vamos utilizar o WolframAlpha para resolver essa integral.

Use o seguinte input: 2πIntegrate[rSqrt[1+ 4r^2Sin[r^2]^2],{r,0,1}]

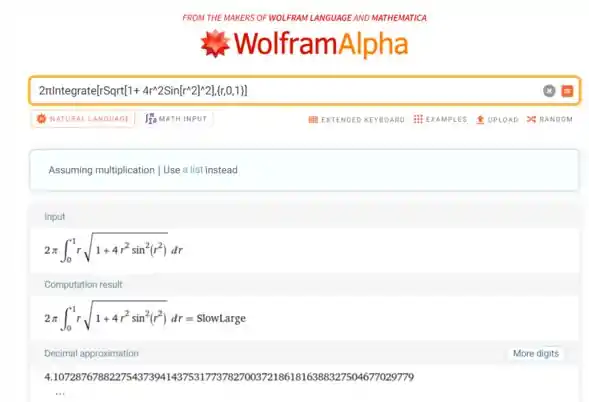
Logo, utilizando quatro casa decimais vamos ter:

A = 2 π ∫ 0 1 r 1 + 4 r 2 s e n 2 r 2   d r ≅ 4,1073

Resposta

A ≅ 4,1073

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície.A parte da esfera x 2 + y 2 + z 2 = b 2 que está dentro do cilindro x 2 + y 2 = a 2 , onde 0ab .
Encontre a área da superfície.A parte do plano x + 2 y + 3 z = 1 que está dentro do cilindro x 2 + y 2 = 3 .
Calcule a integral de superfície. ∬ x y z d S , S é o cone com equações paramétricas x = u c o s v , y = u s e n v , z = v , 0 ≤ u ≤ 1,0 ≤ v ≤ π 2 .
Calcule a integral de superfície. ∬ x z d S , S é a parte do plano 2 x + 2 y + z = 4 que está no primeiro octante.