Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Centro de Massa e Momento de Inércia

Ver Todos os Exercícios

Teoria

Aqui vamos ver uma aplicação física de integral de superfícies, calculando o centro de massa e momento de inércia! Mas antes, vamos relembrar como calcular uma integral de superfície!

Revisão: Integral de superfície

Para o cálculo de integral de superfície é importante seguir alguns passos. Vamos calcular a integral da função f ( x , y , z ) sobre a superfície S .

Passo 1: Parametrizar a superfície S pela função φ ( u , v )

Passo 2: Encontrar o vetor normal à superfície parametrizada e o seu módulo: N →

Passo 3: Resolver a integral

∬ S   f d S = ∬ D   f ( φ u ,   v ) N → d u d v

Esses são os passos básicos para resolver uma integral de superfície!

Centro de Massa

Antes de ver a aplicação da integral de superfície vamos aprender como são definidos o centro de massa e o momento de inércia.

O centro de massa pode ser interpretado como um ponto de equilíbrio do sistema, ou seja, se a massa toda da superfície se concentrasse em um ponto, este ponto seria o centro de massa. Ele é calculado pelas seguintes fórmulas:

x - = ∬ D x δ ( x , y , z ) d S ∬ D δ ( x , y , z ) d S

y - = ∬ D y δ ( x , y , z ) d S ∬ D δ ( x , y , z ) d S

z - = ∬ D z δ ( x , y , z ) d S ∬ D δ ( x , y , z ) d S

Onde δ ( x , y , z ) é a densidade da superfície.

Quando a densidade é constante, ela pode ser retirada da integral. Nesse caso a gente tem o chamado centroide da superfície. Na prática o que iremos calcular é:

x c = ∬ D x δ ( x , y , z ) d S ∬ D δ ( x , y , z ) d S

y c = ∬ D y δ ( x , y , z ) d S ∬ D δ ( x , y , z ) d S

z c = ∬ D z δ ( x , y , z ) d S ∬ D δ ( x , y , z ) d S

Momento de inércia

O momento de inércia é o momento, em relação a um eixo, que aquela superfície teria se toda sua massa estivesse concentrada no centro de massa. Ele depende de um eixo referencial! O momento de inércia em relação a um eixo L é definido por:

I L = ∬ D d 2 x , y , z δ x , y , z d x d y

Onde, d ( x , y , z ) é a distância do ponto x , y , z à reta L .

Caso particular: Geralmente calculamos o momento de inércia em relação aos eixos coordenados x , y e z que são:

I x = ∬ D ( y 2 + z 2 ) δ x , y , z d y d z

I y = ∬ D ( x 2 + z 2 ) δ x , y , z d x d z

I z = ∬ D ( x 2 + y 2 ) δ x , y , z d x d y

Observação: Às vezes é pedido que se calcule o raio de rotação ou de giração. Vamos entender o conceito de raio de rotação! Você tem uma superfície de massa M   e quer calcular o a distância que teríamos que colocar uma fita de massa M , paralela a L , e que tenha o mesmo momento de inércia da sua superfície! O raio de giração é calculado por:

I L = M k L 2

k L = I L M

Exemplo: Encontre o centroide da superfície cortada do cilindro x 2 + y 2 = 9 , pelos planos z = 0 e z = 3 .

Para o cálculo do centro de massa da superfície devemos encontrar:

x c = ∬ D x d S ∬ D d S ,   y c = ∬ D y d S ∬ D d S ,   z c = ∬ D z d S ∬ D d S

Ou seja, devemos resolver quatro integrais de superfície, e para isso devemos seguir os três passos mostrados na revisão de integral de superfície!

Passo 1: Parametrizar a superfície S pela função φ ( θ , t )

Vamos começar parametrizando a superfície! Como temos um cilindro, a parametrização cilíndrica parece ser a certa!

x = 3 cos ⁡ θ y = 3 s en ⁡ θ z = t

Assim a função parametrização é,

φ θ ,   t = ( 3 cos ⁡ θ ,   3 s en ⁡ θ ,   t )  

0 ≤ θ ≤ 2 π

0 ≤ t ≤ 3

Passo 2: Encontrar o vetor normal à superfície parametrizada e o seu módulo: N → θ ,   t

Tendo a função φ , agota temos que calcular o módulo da normal para resolver a integral de superfície!

A normal de uma função parametrizada por φ é:

N → t , θ = ∂ φ ∂ t × ∂ φ ∂ θ

N → t , θ =   i j k 0 0 1 - 3  s en ⁡ θ 3   cos ⁡ θ 0

N → t , θ = ( - 3   cos ⁡ θ , - 3   s en ⁡ θ ,   0 )

Então,

N → t ,   θ = 9 cos 2 ⁡ θ + 9   s e n 2 θ  

Usando a relação fundamental da trigonometria, s e n 2 θ + cos 2 ⁡ θ = 1 , temos:

N → t ,   θ = 9   = 3

Pronto, agora temos o módulo da normal!

Passo 3: Resolver as integrais de superfície

∬ S   f d S = ∬ D   f ( φ u ,   v ) N → u ,   v d u d v

A primeira integral é o denominador comum das três coordenadas do centro de massa!

∬ D d S = 3 ∫ 0 2 π ∫ 0 3 d t d θ = 3 ⋅ 2 π ⋅ 3 = 18 π

Agora vamos calcular cada uma das coordenadas,

x c = ∬ D x d S ∬ D d S = 3 ∫ 0 2 π ∫ 0 3 3 cos ⁡ θ d t d θ 18 π = 3 ∫ 0 2 π 3 ⋅ 3 cos ⁡ θ d t d θ 18 π

x c = 3 9 s en ⁡ θ 0 2 π 18 π = 0

y c = ∬ D y d S ∬ D d S = 3 ∫ 0 2 π ∫ 0 3 3 s en ⁡ θ d t d θ 18 π = 3 ∫ 0 2 π 3 ⋅ 3 s en ⁡ θ d t d θ 18 π

y c = 3 - 9 cos ⁡ θ 0 2 π 18 π = 0

z c = ∬ D z d S ∬ D d S = 3 ∫ 0 2 π ∫ 0 3 t d t d θ 18 π = 3 ⋅ 2 π ⋅ t 2 2 0 3 18 π

z c = 6 π ⋅ 9 2 18 π = 3 2

Resposta:

Assim, o centro de massa da superfície é o ponto:

C . M .   =   0 ,   0 , 3 2

Exemplo: Agora vamos considerar a mesma superfície com densidade constante δ , de o momento de inercia em relação ao eixo x e seu raio de giração.

Para isso, devemos usar as fórmulas,

I x = ∬ D ( y 2 + z 2 ) f x , y , z d S

k x = I x M ,     M = ∬ D f x , y , z d S

Como a densidade é constante δ :

f x ,   y , z = δ  

Ou seja, devemos resolver integrais de superfície e para isso seguir os três passos fundamentais!

Passo 1: Parametrizar a superfície S pela função φ ( θ , t )

Vamos começar parametrizando a superfície! Como temos um cilindro, a parametrização cilíndrica parece ser a certa!

x = 3 cos ⁡ θ y = 3 s en ⁡ θ z = t

Assim a função parametrização é,

φ θ ,   t = ( 3 cos ⁡ θ ,   3 s en ⁡ θ ,   t )  

0 ≤ θ ≤ 2 π

0 ≤ t ≤ 3

Passo 2: Encontrar o vetor normal à superfície parametrizada e o seu módulo: N → θ ,   t

Tendo a função φ , agota temos que calcular o módulo da normal para resolver a integral de superfície!

A normal de uma função parametrizada por φ é:

N → t , θ = ∂ φ ∂ t × ∂ φ ∂ θ

N → t , θ =   i j k 0 0 1 - 3  s en ⁡ θ 3   cos ⁡ θ 0

N → t , θ = ( - 3  cos ⁡ θ , - 3   sen ⁡ θ ,   0 )

Então,

N → t ,   θ = 9 cos 2 ⁡ θ + 9   s e n 2 θ  

Usando a relação fundamental da trigonometria, s e n 2 θ + cos 2 ⁡ θ = 1 , temos:

N → t ,   θ = 9   = 3

Pronto, agora temos o módulo da normal!

Passo 3: Resolver as integrais de superfície usando

∬ S   f d S = ∬ D   f ( φ u ,   v ) N → u ,   v d u d v

A primeira integral é momento de inércia me relação a x !

I x = ∬ D ( y 2 + z 2 ) f x , y , z d S

I x = δ ∫ 0 2 π ∫ 0 3 9 s en 2 ⁡ θ + t 2 3 d t d θ

Integrando em relação a t

= 3 δ ∫ 0 2 π t 9 s en 2 ⁡ θ + t 3 3 t = 0 t = 3 d θ =

= 3 δ ∫ 0 2 π 27 s en 2 ⁡ θ + 9 d θ

Para resolver esta integral vamos usar a definição de arco duplo,

s en 2 ⁡ θ = ( 1 - cos ⁡ 2 θ ) 2  

Assim a integral fica,

I x = 3 δ ∫ 0 2 π 27 ( 1 - cos ⁡ 2 θ ) 2 + 9 d θ = 3 δ 27 θ 2 - 27 sen ⁡ 2 θ 4 + 9 θ θ = 0 θ = 2 π =

= 3 δ 27 π + 18 π = 3 δ 45 π = 135 π δ

I x = 135 π δ

Passo 4:

Agora para calcular o raio de giração, precisamos calcular a massa

    M = ∬ D f x , y , z d S = δ ∫ 0 2 π ∫ 0 3 3 d t d θ = 3 δ ⋅ 2 π ⋅ 3 = 18 π δ

Por fim, o raio de giração é

k x = I x M = 135 π δ 18 π δ   = 15 2 = 30 2    

k x = 30 2

Momento de inércia

Exercícios Resolvidos

Exercício Resolvido #1

Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1154 - 29

O centroide de um superfície σ é definido por

x - = ∬ σ x d S á r e a   d e   σ ,   y - = ∬ σ y d S á r e a   d e   σ ,   z - = ∬ σ z d S á r e a   d e   σ

Encontre o centroide da superfície na porção do paraboloide

z = 1 2 x 2 + y 2

Abaixo do plano z = 4 .

Passo 1

Temos algumas integrais de superfície para resolver.

A Primeira coisa que temos que fazer é parametrizar a superfície! Como é um paraboloide, a parametrização vai ser semelhante a cilíndrica:

x = R s e n θ y = R c o s θ z = t

Vamos substituir na equação para deixarmos somente em função de dois parâmetros:

t = 1 2 ( R 2 s e n 2 θ + R 2 cos 2 ⁡ θ )  

2 t = R 2 ( s e n 2 θ + cos 2 ⁡ θ )

Usando a relação fundamental da trigonometria s e n 2 θ + cos 2 ⁡ θ = 1

2 t = R 2

R = 2 t

Assim temos como função paramétrica:

φ t , θ = ( 2 t s e n θ ,   2 t c o s θ ,   t )

Passo 2

Tendo a função φ , agota temos que calcular o módulo da normal para resolver a integral de superfície!

A normal de uma função parametrizada por φ é:

N → t , θ = ∂ φ ∂ t × ∂ φ ∂ θ

N → t , θ =   i j k 1 / 2 t sen ⁡ θ 1 / 2 t cos ⁡ θ 1 2 t cos ⁡ θ - 2 t sen ⁡ θ 0

N → t , θ = ( 2 t sen ⁡ θ ,   2 t cos ⁡ θ ,   - s e n 2 θ - cos 2 ⁡ θ )

Usando a relação fundamental da trigonometria, s e n 2 θ + cos 2 ⁡ θ = 1 , temos:

N → t , θ = ( 2 t sen ⁡ θ ,   2 t cos ⁡ θ ,   - 1 )  

Então,

N → t ,   θ = 2 t s e n 2 θ + 2 t cos 2 ⁡ θ + 1  

Usando a relação fundamental da trigonometria, s e n 2 θ + cos 2 ⁡ θ = 1 , temos:

N → t ,   θ = 2 t + 1  

Pronto, agora temos o módulo da normal!

Passo 3

Agora vamos definir os intervalos de integração:

Como z = 1 2 ( x 2 + y 2 ) , ou seja, a soma de dois quadrados, temos que:

z ≥ 0

E o enunciado diz que a superfície é a parte do paraboloide que está abaixo do plano z = 4 , e como z = t , temos:

0 ≤ t ≤ 4

0 ≤ θ ≤ 2 π

Passo 4

Vamos calcular cara uma das integrais, começando pela área que é comum a todas as coordenadas:

A = ∫ 0 2 π ∫ 0 4 2 t + 1   d t d θ      

Para resolver esta integral faremos,

u = 2 t + 1

d u = 2 d t

Substituindo a integral fica,

A = ∫ 0 2 π ∫ 1 9 u   2 d u d θ    

A = ∫ 0 2 π 1 2 2 u 3 / 2 3 1 9 d θ = 2 π 26 3 = 52 π 3  

A = 52 π 3

Calculando as coordenadas:

x - A = ∫ 0 4 ∫ 0 2 π 2 t s e n θ 2 t + 1   d θ d t    

x - A = ∫ 0 4 2 t 2 t + 1   - c o s θ 0 2 π d t  

x - A = ∫ 0 4 2 t 2 t + 1   ( 0 ) d t   = 0

x - = 0

y - A = ∫ 0 4 ∫ 0 2 π 2 t c o s θ 2 t + 1   d θ d t    

y - A = ∫ 0 4 2 t 2 t + 1   s e n θ 0 2 π d t  

y - A = ∫ 0 4 2 t 2 t + 1   ( 0 ) d t   = 0

y - = 0

z - A = ∫ 0 4 ∫ 0 2 π t 2 t + 1   d θ d t    

Novamente vamos fazer a substituição,

u = 2 t + 1

d u = 2 d t

Substituindo a integral fica,

z - A = 2 π ∫ 1 9 u 2 u - 1 2 d u  

z - A = 2 π ⋅ 1 4 2 u 5 2 5   + 2 u 2 3 3 1 9 = π 2 2 ⋅ 3 5 5 - 2 ⋅ 3 2 3 - 2 ⋅ 1 5 5 + 2 ⋅ 1 2 3 = π 2 1192 15   = 596 π 15

z - 52 π 3 = 596 π 15

z - = 149 65

Resposta

Então, o centroide é

x - ,   y - ,   z - = 0 ,   0 , 149 65

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 266- 4.

Sabendo que o centro de massa ( x c ,   y c ,   z c ) de uma superfície S é definido por

x c = ∬ S x f ( x , y , z ) d S M ,   y c = ∬ S y f ( x , y , z ) d S M ,   z c = ∬ S z f ( x , y , z ) d S M

Onde M é a massa total de S   e f ( x , y , z ) é a densidade em cada ponto x ,   y ,   z ∈ S , calcule o centro de massa das seguintes superfícies com densidade constante.

  1. S tem representação paramétrica φ u , v = ( u , v , u 2 + v 2 ) , u 2 + v 2 ≤ 1 .
  2. S é a parte da superfície cônica z 2 = x 2 + y 2 compreendida entre os planos z = 1 e z = 2

Passo 1

(a) Sabemos que a superfície tem representação paramétrica explicita,

φ u , v = ( u , v , u 2 + v 2 ) , u 2 + v 2 ≤ 1 .

Assim, o módulo sua normal é dado por:

N → ( u ,   v ) = ∂ f ∂ u 2 +   ∂ f ∂ v 2 + 1

N → ( u ,   v ) = 4 u 2 + 4 v 2 + 1

Passo 2

Primeiro vamos calcular a massa, para isso devemos usar que a densidade f x ,   y ,   z = k , que é contante. Asism,

M = ∬ S k d S  

M = ∬ D k 4 u 2 + 4 v 2 + 1 d u d v    

Passo 3

Calculando o centro de massa,

x c = ∬ D u k 4 u 2 + 4 v 2 + 1 d u d v ∬ D k 4 u 2 + 4 v 2 + 1 d u d v  

Para simplificar a integral, vamos fazer a seguinte substituição: u = r c o s θ e v = r s e n θ ,

u 2 + v 2 = r 2 s e n 2 θ + r 2 cos 2 ⁡ θ  

Usando a relação fundamental da trigonometria s e n 2 θ + cos 2 ⁡ θ = 1 ,

u 2 + v 2 = r 2

Então a integral fica,

x c = ∫ 0 2 π ∫ 0 1 r c o s θ 4 r 2 + 1 r d r d θ ∫ 0 2 π ∫ 0 1 4 r 2 + 1 r d r d θ

Como ∫ 0 2 π c o s θ d θ = 0 ,

x c = 0

Agora vamos calcular o y c ,

y c = ∬ S y f ( x , y , z ) d S M

y c = ∬ D v k 4 u 2 + 4 v 2 + 1 d u d v ∬ D k 4 u 2 + 4 v 2 + 1 d u d v  

Fazendo a mesma substituição u = r c o s θ e v = r s e n θ , temos:

y c = ∫ 0 2 π ∫ 0 1 r s e n θ 4 r 2 + 1 r d r d θ ∫ 0 2 π ∫ 0 1 4 r 2 + 1 r d r d θ

Como ∫ 0 2 π s e n θ d θ = 0 ,

y c = 0

Por último, vamos calcular a coordenada z c ,

z c = ∬ S z f ( x , y , z ) d S M

z c = ∬ D u 2 + v 2 k 4 u 2 + 4 v 2 + 1 d u d v ∬ D k 4 u 2 + 4 v 2 + 1 d u d v  

Novamente, fazendo a mesma substituição u = r c o s θ e v = r s e n θ , temos:

z c = ∫ 0 2 π ∫ 0 1 r 2 4 r 2 + 1 r d r d θ ∫ 0 2 π ∫ 0 1 4 r 2 + 1 r d r d θ

z c = 2 π ∫ 0 1 r 2 4 r 2 + 1 r d r 2 π ∫ 0 1 4 r 2 + 1 r d r

Resolver essa integral não ficou muito fácil, vamos resolver a integral no próximo passo e depois voltamos para encontrar o valor de z c .

Passo 4

Para resolver a integral vamos fazer a substituição de variáveis, t 2 = 4 r 2 + 1 , assim:

t 2 - 1 = 4 r 2 → r 2 = t 2 - 1 4

2 t d t =   8 r d r → r d r = t d t 4

Assim,

∫ 0 1 r 2 4 r 2 + 1 r d r = ∫ 1 5 t 2 - 1 4 t × t 4 d t

∫ 1 5 t 2 - 1 4 t d t = 1 16 t 5 5 - t 3 3 1 5 = 1 16 25 5 5 - 5 5 3 - 1 5 + 1 3 = 1 240 ( 50 5 + 2 )

Ainda,

∫ 1 5 4 r 2 + 1 r d r = ∫ 1 5 t × t 4 d t = 1 4 t 3 3 1 5

∫ 1 5 t × t 4 d t = 1 4 t 3 3 1 5 = 1 4 5 5 3 - 1 3 = 1 12 ( 5 5 - 1 )

Voltando ao cálculo de z c , temos:

z c = 1 240 50 5 + 2 1 12 ( 5 5 - 1 ) = 25 5 + 1 10 ( 5 5 - 1 )

Passo 5

(b) Parametrizando z 2 = x 2 + y 2 , podemos usar a parametrização explícita e como z   é positivo (parte da cônica entre os plano z = 1 e z = 2 ):

z = f x , y = x 2 + y 2

A equação parametrizada será,

φ u ,   v = ( u ,   v ,   u 2 + v 2 )

Assim, o módulo sua normal é dado por:

N → ( u ,   v ) = ∂ f ∂ u 2 +   ∂ f ∂ v 2 + 1

N → ( u ,   v ) = u 2 u 2 + v 2 + v 2 u 2 + v 2 ⏟ 1 + 1

N → ( u ,   v ) = 2

Passo 6

Calculando o centro de massa,

x c = ∬ D u k 2 d u d v ∬ D k 2 d u d v  

Aplicando os limites de z do enunciado, vemos que:

1 ≤ z ≤ 2

1 ≤ u 2 + v 2 ≤ 2

1 ≤ u 2 + v 2 ≤ 4

Pra colocar isso nos limites, vamos fazer a seguinte substituição:

u = r c o s θ

v = r s e n θ

Com isso os limites são:

1 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

Então a integral fica,

∬ D u k 2 d u d v ∬ D k 2 d u d v   = k 2 ∫ 0 2 π ∫ 1 2 r cos ⁡ θ d r d θ k 2 ∫ 0 2 π ∫ 1 2 1 d r d θ

A integral do numerador é zero porque

∫ 0 2 π cos ⁡ θ d θ = 0

Já a integral do denominador, que é a massa total, fica

M = k 2 ∫ 0 2 π ∫ 1 2 1 d r d θ = k 2 2 - 1 2 π

M = 2 2 k π

Agora vamos calcular o y c ,

y c = ∬ S y f ( x , y , z ) d S M

y c = ∬ D v k 2 d u d v 2 2 k π

Fazendo a mesma substituição u = r c o s θ e v = r s e n θ , temos:

y c = ∫ 0 2 π ∫ 1 2 r s e n θ 2 r d r d θ 2 2 k π

Como ∫ 0 2 π s e n θ d θ = 0 ,

y c = 0

Por último, vamos calcular a coordenada z c ,

z c = ∬ S z f ( x , y , z ) d S M

z c = ∬ D u 2 + v 2 k 2 d u d v 2 2 k π

Novamente, fazendo a mesma substituição u = r c o s θ e v = r s e n θ , temos:

z c = ∫ 0 2 π ∫ 1 2 r 2 k 2 r d r d θ 2 2 k π

Calculando essa integral do numerador, temos

k 2 ∫ 0 2 π ∫ 1 2 r 2 d r d θ = 2 π r 3 3 1 2 k 2 =

2 2 k π 8 - 1 3   = 14 2 3 k π

Juntando esse resultado com aquele denominador M

z c = 14 2 3 k π 2 2 k π = 7 3

Resposta

(a)

0 ,   0 ,   25 5 + 1 10 5 5 - 1

(b)

0 , 0 , 7 3

Exercício Resolvido #3

George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education Brasil ltda., 2009, pp. 516-36.

Encontre o momento de inércia em relação ao eixo z de uma casca fina de densidade constante δ cortada do cone 4 x 2 + 4 y 2 - z 2 = 0 ,   z ≥ 0 , pelo cilindro circular x 2 + y 2 = 2 x

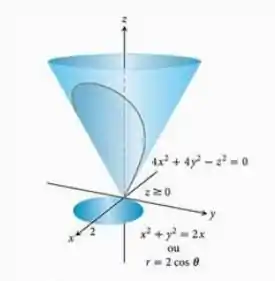
Passo 1

Para encontrar o momento de inércia devemos calcular:

I z = ∬ D ( x 2 + y 2 ) δ d S

Para resolver esta integral devemos saber o módulo do vetor normal à superfície e para isto vamos parametrizar ela.

Podemos usar a parametrização:

x = r s e n θ y = r c o s θ z = 2 r

Assim a superfície é parametrizada por,

φ r ,   θ = ( r s e n θ ,   r c o s θ ,   2 r )

Passo 2

Encontrando o módulo do vetor normal,

N → r ,   θ = ∂ φ ∂ r × ∂ φ ∂ θ

N → ( r ,   θ ) =   i j k s e n θ c o s θ 2 r c o s θ r s e n θ 0

N → r ,   θ = ( 2 r s e n θ ,   2 r c o s θ ,   - r )

N → r ,   θ = 4 r 2 s e n 2 θ + 4 r 2 cos 2 ⁡ θ + r 2

Usando a relação fundamental da trigonometria s e n 2 θ + cos 2 ⁡ θ = 1 ,  

N → r ,   θ = 5 r 2 = r 5

Passo 3

Agora vamos resolver a integral de superfície,

I z = ∬ D ( x 2 + y 2 ) δ d S

Como δ é constante:

I z = δ ∬ S ( r 2 s e n 2 θ + r 2 cos 2 ⁡ θ ) r 5 d r d θ

I z = δ 5 ∬ S r 3 d r d θ

Queremos a parte da cônica que se encontra dentro do cilindro r = 2 s e n θ

I z = δ 5 ∫ - π / 2 π / 2 ∫ 0 2 c o s θ r 3 d r d θ

I z = δ 5 ∫ - π / 2 π / 2 ∫ 0 2 c o s θ r 3 d r d θ

I z = δ 5 ∫ - π / 2 π / 2 r 4 4 0 2 c o s θ d θ = δ 5 ∫ - π / 2 π / 2 1 4 16 cos 4 ⁡ θ d θ = 4 δ 5 ∫ - π / 2 π / 2 cos 4 ⁡ θ d θ  

Esta integral é difícil de resolver, vamos resolver ela no próximo passo e depois voltamos para terminar o exercício!

Passo 4

Para resolver esta integral, vamos utilizar a seguinte igualdade trigométrica:

c o s 2 θ = 2 cos 2 ⁡ θ - 1 → cos 2 ⁡ θ = cos ⁡ 2 θ + 1 2  

Assim, temos que:

cos 4 ⁡ θ = cos ⁡ 2 θ + 1 2 4   = cos 2 ⁡ 2 θ + 2 cos ⁡ 2 θ + 1 4

Integrando,

∫ - π / 2 π / 2 c o s 4 θ d θ = 1 4 ∫ - π / 2 π / 2 ( cos 2 ⁡ 2 θ + 2 cos ⁡ 2 θ + 1 ) d θ

Mas,

cos 2 ⁡ 2 θ = cos ⁡ 4 θ + 1 2

Substituindo,

∫ - π / 2 π / 2 c o s 4 θ d θ = 1 4 ∫ - π / 2 π / 2 cos ⁡ 4 θ + 1 2 + 2 cos ⁡ 2 θ + 1 d θ

∫ - π / 2 π / 2 c o s 4 θ d θ = 1 4 ∫ - π / 2 π / 2 cos ⁡ 4 θ + 4 cos ⁡ 2 θ + 3 2 d θ

Como,

∫ cos ⁡ n θ d θ = sen ⁡ n θ n + C

∫ - π 2 π 2 c o s 4 θ d θ = 1 8 sen ⁡ 4 θ 4 + 4 sen ⁡ 2 θ 2 + 3 θ - π 2 π 2 = 3 π 8

Passo 5

Voltando ao nosso problema, temos:

I z =   4 δ 5 ∫ - π / 2 π / 2 cos 4 ⁡ θ d θ

Substituindo o resultado encontrado,

I z =   4 δ 5 ⋅ 3 π 8 = 3 π δ 5 2

Resposta

I z = 3 π δ 5 2

Exercício Resolvido #4

George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education Brasil ltda., 2009, pp. 516-35.

Encontre o centro de massa, o momento de inércia e o raio de rotação em relação ao eixo z   de uma casca fina de densidade constante δ cortada do cone x 2 + y 2 - z 2 = 0 pelo planos z = 1 e z = 2 .

Passo 1

Pela simetria da superfície, x c = 0 e y c = 0 . Agora falta calcularmos, z c . Primeiro vamos calcular a massa M :

∬ S δ d S = δ ∬ S d S

Passo 2

Para resolver esta integral devemos saber o módulo do vetor normal à superfície e para isto vamos parametrizar ela.

Podemos usar a parametrização:

x = r s e n θ y = r c o s θ z = r

Assim a superfície é parametrizada por,

φ r ,   θ = ( r s e n θ ,   r c o s θ ,   r )

Passo 3

Encontrando o módulo do vetor normal,

N → r ,   θ = ∂ φ ∂ r × ∂ φ ∂ θ

N → ( r ,   θ ) =   i j k s e n θ c o s θ 1 r c o s θ r s e n θ 0

N → r ,   θ = ( r s e n θ ,   r c o s θ ,   - r )

N → r ,   θ = r 2 s e n 2 θ + r 2 cos 2 ⁡ θ + r 2

Usando a relação fundamental da trigonometria s e n 2 θ + cos 2 ⁡ θ = 1 ,  

N → r ,   θ = 2 r 2 = r 2

Passo 4

Para encontrar o centro de massa:

M = δ ∬ S d S = δ 2 ∫ 0 2 π ∫ 1 2 r d r d θ

M = δ 2 × 2 π r 2 2 1 2 = 3 2 π δ

Assim,

z c = δ ∬ S z d S M

z c =   δ 2 ∫ 0 2 π ∫ 1 2 r 2 d r d θ 3 2 π δ

z c =   2 π r 3 3 1 2 3 π = 2 3 × 7 3

z c = 14 9

Logo,

C M = 0 ,   0 , 14 9  

Passo 5

Para encontrar o momento de inércia devemos calcular:

I z = ∬ D ( x 2 + y 2 ) δ d S

Agora vamos resolver a integral de superfície,

I z = ∬ D ( x 2 + y 2 ) δ d S

Como δ é constante:

I z = δ ∬ S ( r 2 s e n 2 θ + r 2 cos 2 ⁡ θ ) r 2 d r d θ

I z = δ 2 ∬ S r 3 d r d θ

Queremos a parte da cônica que se encontra dentro do cilindro r = 2 s e n θ

I z = δ 2 ∫ 0 2 π ∫ 1 2 r 3 d r d θ

I z = δ 2 × 2 π r 4 4 1 2 = 15 π 2 2 δ

Passo 6

O raio de rotação é definido como:

I z = M R 2

R 2 = 1 M 15 π 2 2 δ

Como M = 3 π 2 δ

R 2 = 1 3 π 2 δ 15 π 2 2 δ

R 2 = 5 2

R = 10 2

Resposta

Centro de Massa:

C M = 0 ,   0 , 14 9  

Momento de Inércia em relação a z:

I z = 15 π 2 2 δ

Raio de rotação em relação a z:

R = 10 2

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .