Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 15
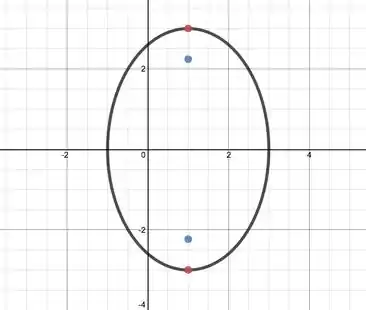
Encontre os vértices e os focos da elipse e esboce o seu gráfico.
Passo 1
Olá, meu brother. Vou te ajudar a resolver essa atividade hoje.
Nessa questão, nos foi dada a equação de uma elipse
para encontrarmos seus vértices e focos.
Para resolvermos essa atividade iremos organizar essa equação geral em um formato de equação de elipse que a gente já conhece.
A equação geral de uma elipse é
e quando temos o número maior embaixo do esta é uma elipse com eixo maior no eixo .
O foco de uma elipse desse tipo é dado por
E os vértices são:
Passo 2
Primeiramente vamos ajeitar a equação:
Colocando em evidência:
Organizando de forma a gerar um produto notável:
Completando o quadrado:
Vamos dividir ambos os lados por :
Então temos que o foco é:
Os vértices da elipse
são:
Então,
Passo 3
Vamos esboçar essa elipse:
Os pontos vermelhos são vértices.
Os pontos azuis são focos.
