Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 9
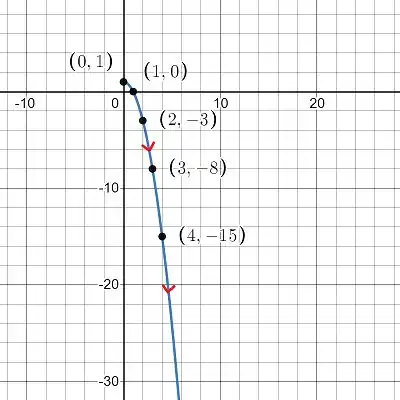
A ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta
B ) Elimine os parâmetros para encontrar uma equação cartesiana da curva
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade.
Aqui a gente tem a curva parametrizada:
E vamos criar o gráfico dessa curva marcando pontos em um gráfico. Para isso, a gente vai criar uma tabela, onde colocaremos valores de e seus respectivos valores de e , que são dependentes de .
Já na letra b), o que iremos fazer para colocarmos nossa curva em coordenadas cartesianas é isolar o valor de em uma das duas curvas, e substituirmos na outra.
Então podemos isolar o em e depois iremos colocar esse valor de em .
Passo 2
Essa é um exercício que te ajuda a criar gráficos. Algo muito importante, principalmente quando formos avançando e chegando por exemplo em cálculo 3.
Vamos fazer o seguinte, vamos criar uma tabela com valores de e plotar esses pontos num gráfico.
Beleza, tendo esses pontos, já podemos criar os gráficos. Antes vamos olhada nas nossas funções
Percebeu que estamos tratando com uma das equações com parâmetro t tem raiz quadrada? Isso quer dizer que nossa função é uma semi-parábola.
Show? Vamos plotar nossos pontos e criar o gráfico
Passo 3
Utilizando o GeoGebra para plotarmos os pontos e criarmos o nosso gráfico:
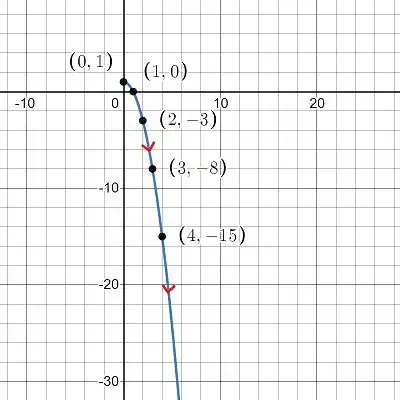
Podemos perceber que conforme t cresce y decresce.
Passo 4
Letra b)
Agora vamos voltar do mundo paramétrico para o cartesiano. A melhor solução para isso é isolar alguma das variáveis e substituir na outra.
Matematicamente será bem tranquilo, mas você vai precisar de uma intuição para qual a melhor variável para isolar seja ela ou .
Vamos cair dentro então:
Está vendo que está mais facil? Vou isolar ele então:
Substituindo em
Isso deixa bem evidente a parábola com eixo em , sendo que como tínhamos , então isso quer dizer que so podemos ter .
Bem, terminamos por aqui. Esses exercícios estão no início bem intuitivos, com o tempo vamos aprender mais ferramentas para construir gráficos. Te vejo na próxima resolução: )
