Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 10
10. Expresse o comprimentro do lado de um quadrado em função do comprimento da diagonal do quadrado. Depois, expresse a área do quadrado em função do comprimento da diagonal.
Passo 1
Usando pitagoras conseguimos calcular o comprimento do lado do quadrado:
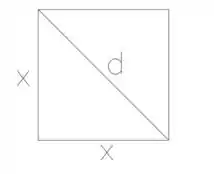
Passo 2
Agora, como já temos o comprimento do lado do quadrado conseguimos calcular sua área:
Resposta
Exercícios de Livros Relacionados
Encontre uma equação da forma y = k x 2 + b x + c cujo gráfico se adeque razoavelmente com o da figura abaixo. Confira seu trabalho com um recurso gráfico.
Encontre uma equação da forma y = D + A s e n ( B x ) ou y = D + A c o s ( B x ) para cada gráfico.
Encontre uma equação da forma y = D + A s e n ( B x ) ou y = D + A c o s ( B x ) para cada gráfico.
Encontre uma equação da forma y = y 0 + A s e n B x - C para cada gráfico.
Nos EUA, as tomadas elétricas padrão fornecem uma corrente elétrica senoidal com uma voltagem máxima de V = 120 2 volts (V), a uma frequência de 60 hertz (Hz). Escreva uma equação que expresse Vcomo u