Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 31
Encontre uma equação da forma ou para cada gráfico.
Passo 1
Nesse exercício, vamos identificar o período e a amplitude de cada gráfico
Sabendo que o período é dado pelo tamanho de uma onda completa () e a amplitude () é a metade da oscilação da função. Vamos ver isso melhor na prática!
Passo 2
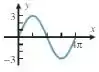
(a) Vamos olhar para o gráfico de novo:
Fica uma dica: como o gráfico parte da origem, é mais fácil usarmos o seno para descrevê-lo. Isso porque , ok?
Podemos ver que a função tem seu valor mínimo em e máximo em , logo, sua oscilação é . Com isso, já sabemos sua amplitude:
Além disso, vemos que o tamanho dela é de , logo, esse é o valor do período:
Até agora temos:
E o valor de ? Vamos usar a informação de que a função passa por , substituindo isso em :
Nossa função, então, é:
Passo 3
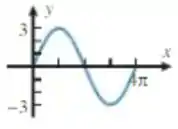
(b) Vamos olhar para o gráfico de novo:
Fica uma dica: como o gráfico não parte da origem, é mais fácil usarmos o cosseno para descrevê-lo. Isso porque , ok?
Podemos ver que a função tem seu valor mínimo em e máximo em , logo, sua oscilação é . Com isso, já sabemos sua amplitude:
Além disso, vemos que o tamanho dela é de , logo, esse é o valor do período:
Até agora temos:
E o valor de ? Vamos usar a informação de que a função passa por , substituindo isso em :
Nossa função, então, é:
Passo 4
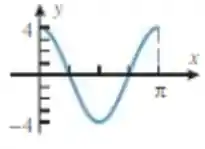
(c) Vamos olhar para o gráfico de novo:
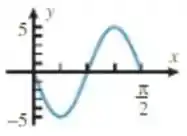
Fica uma dica: como o gráfico parte da origem, é mais fácil usarmos o seno para descrevê-lo. Isso porque , ok?
Podemos ver que a função tem seu valor mínimo em e máximo em , logo, sua oscilação é . Com isso, já sabemos sua amplitude:
Além disso, vemos que o tamanho dela é de , logo, esse é o valor do período:
Até agora temos:
E o valor de ? Vamos usar a informação de que a função passa por , substituindo isso em :
Nossa função, então, é:
Resposta
(a)
(b)
(c)