Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 11
11. Expresse o comprimentro da aresta de um cubo em função do comprimento da diagonal . Depois, expresse a área da superfície e o volume do cubo em função do comprimento da diagonal.
Passo 1
Para nós conseguirmos achar o valor da aresta, , precisamos usar pitagoras no triângulo ACD, porém não temos o valor de .
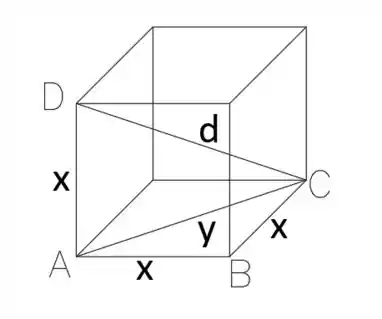
Então precisamos calcular ele primeiro, usando pitagoras no triângulo ABC:
Passo 2
Agora, como já temos o conseguimos calcular em função de usando pitagoras no triangulo ACD:
Passo 3
A superfície do cubo é formada por 6 quadrados, então devemos achar a área desse quadrado e multiplicar ele por 6:
Passo 4
O volume do cubo é igual a sua aresta ao cubo:
Resposta
Exercícios de Livros Relacionados
Esboce um gráfico da temperatura externa como uma função do tempo durante um dia típico de primavera.
Esboce um gráfico do valor de mercado de um carro novo como função do tempo por um período de 20 anos. Suponha que ele esteja bem conservado.
Um homem apara seu gramado toda quarta-feira à tarde. Esboce o gráfico da altura da grama como uma função do tempo no decorrer de um período de quatro semanas.
Coloque uma torta gelada em um forno e asse-a por uma hora. Então tire-a do forno e deixe-a esfriar antes de comê-la. Descreva como varia no tempo a temperatura da torta. Esboce um gráfico da temperat
Esboce o gráfico da quantidade de uma marca particular de café vendida por uma loja como função do preço do café.