Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 17
Esboce um gráfico da temperatura externa como uma função do tempo durante um dia típico de primavera.
Passo 1
E aí! tudo certinho? 👀
O enunciado pede pra a gente esboçar o gráfico da temperatura em função do tempo durante um dia típico de primavera.
Então vamos pensar como podemos fazer isso! Sabemos que:
- A temperatura depende da incidência de luz solar, quanto maior a incidência maior será a temperatura. Assim a maior temperatura vai acontecer próxima a meio dia
- Seguindo o mesmo raciocínio, a temperatura mais fria do dia vai ser o momento em que estamos a mais tempo longe da luz solar. Ou seja, logo antes do sol nascer.
- Após é o momento que começamos a nos “afastar” do sol, portanto a temperatura irá diminuindo até logo antes do sol nascer, no dia seguinte.
Ahh, temos que ter em mente que as condições climáticas variam muito em relação a sua localização!
Bora lá! 😉
Passo 2
É claro que não tem como a gente desenhar um gráfico rigoroso, mas reunindo as informações acima podemos desenhar:
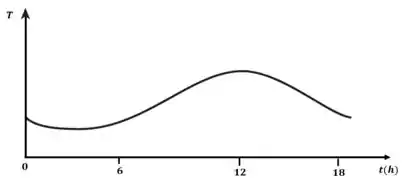
E aí! entendeu tudo? Responde Aí! 😬
Resposta
Exercícios de Livros Relacionados
Calcule a distância entre os pontos dados. 1,2 e 2,3
Calcule a distância entre os pontos dados. - 2,3 e 1,4
Considere a função f x = m á x x , 1 x á .Calcule f 2 , f - 1 e f 1 2 Dê o domínio e esboce o gráfico
Considere a função f x = m á x n ∈ Z | n ≤ x á . (Função maior inteiro.)Calcule f 1 2 , f 1 , f 5 4 e f - 1 5 Esboce o gráfico
Um móvel desloca-se (em movimentoretilíneo) de 0,0 a x , 10 com velocidade constante de 1 (m/s); em seguida, de x , 10 a 30,10 (em movimentos retilíneo) com velocidade constante de 2 (m/s). Expresse o