Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 9
Encontre uma equação da parábola. A seguir, ache o foco e a diretriz.
Passo 1
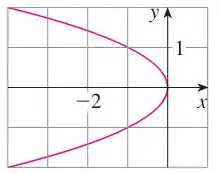
Eaee, belezinha?? Bom... queremos encontrar a equação da seguinte parábola:
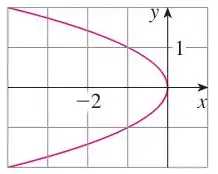
Para isso, primeiramente precisamos definir sua equação padrão analisando para onde está sua concavidade.
A parábola está voltada para cima ou para baixo quando e está voltada para a direita ou para a esquerda quando .
Mas quem é esse ??
Esse parâmetro é que nos vai dizer onde está o vértice, o foco e a diretriz.
O parâmetro é a distância entre o vértice da parábola e o foco ao longo do eixo .
Se a parábola está voltada para cima ou para baixo, o foco está localizado em , e se a parábola está voltada para a esquerda ou para a direita, o foco está localizado em .
E a diretriz??
Se a parábola está voltada para cima ou para baixo (isto é, na forma ), a diretriz é uma reta horizontal localizada a uma distância abaixo do vértice.
Se a parábola está voltada para a direita ou para a esquerda (ou seja, na forma ), a diretriz é uma reta vertical localizada a uma distância à esquerda do vértice.
Passo 2
Analisando a figura, podemos concluir que forma geral de uma parábola desse tipo é da forma:
Pelo passo 1, vemos que um ponto que pertence à parábola é , dessa forma podemos encontrar :
Ainda pelo passo 1, podemos concluir que:
- O seu foco é dado por ;
- e sua diretriz é .
Resposta
O seu foco é dado por e sua diretriz é .