Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 12
12- a) Encontre a excentricidade, b) identifique a cônica, c) dê uma equação da diretriz e d) esboce a cônica.
Passo 1
Eaee, belezinha? Bom... o enunciado nos deu a seguinte equação de uma cônica:
Primeiramente queremos encontrar a sua excentricidade . (Lembre-se que a excentricidade serve para nos dizer o quão "alongada" ou "achatada" é a forma da cônica.).
Para isso, vamos comparar a nossa equação com a seguinte equação geral:
Onde é a diretriz.
Com o valor da excentricidade, iremos identificar a cônica, onde:
- Se , trata-se de uma elipse;
- Se , trata-se de uma parábola;
- Se , trata-se de uma hipérbole.
Com a curva identificada, poderemos analisar e mostrar a equação da diretriz .
Por fim, iremos plotar a nossa curva. Agora bora lá!! 😉
Passo 2
Para adequar a questão do enunciado a da fórmula do passo nós teremos que dividir o numerador e o denominador por . Logo:
Agora comparando as duas equações nós podemos concluir que:
E
E, como , a equação dada é a de uma hipérbole. O sinal não importa muito para dizermos se temos uma parábola, uma hipérbole ou uma elipse.
Note que esse passo responde a letra e a letra .
Passo 3
(c) Show! Pra descobrir a reta diretriz, veja que a equação da cônica tem “” , então a equação da reta é da forma:
Show! Agora só falta descobrir quem é , e isso a gente faz comparando os numeradores:
Como sabemos também que , então:
Então, a equação da reta diretriz fica assim:
Isso nos diz que temos uma hipérbole horizontal. Por que essa é uma reta vertical. Isso nos responde a letra .
Passo 4
Agora para desenhar a cônica devemos saber os vértices, as assíntotas e o centro dessa hipérbole.
E note que pela equação podemos dizer que o denominador será m��nimo quando dando assim nosso vértice máximo (pois está orientado em relação a origem do plano cartesiano de um ângulo ).
Por outro lado, o denominador será máximo com , tendo assim o vértice mínimo.
Logo teremos como vértices:
E
Pontos esses em coordenadas polares! Isso que é importante entender aqui. 😉
Onde a conversão de um ponto em coordenada polar para um ponto em coordenada cartesiana é dada por:
Somando os dois vértices (transformando para cartesiano e dividindo por dois e depois passando para polar de novo) nós teremos um centro em:
Centro em coordenadas cartesianas.
Passo 5
Para encontrar as retas assíntotas nós devemos pensar em encontrar qual o ângulo cujo tenderá a infinito, uma vez que nunca teremos um valor de que pertence a essa reta.
E para isso temos que fazer se aproximar de (para encontrar as duas retas assíntotas) ao fazer tender a zero pela esquerda e pela direita. Da seguinte forma:
Ou seja, o ângulo a partir do centro será de:
E assim como temos para coordenada cartesiana a equação de uma reta sendo como:
Com e sendo pontos quaisquer dessa reta e a angulação da reta em relação ao eixo , então:
Com qualquer e as coordenadas cartesianas do centro da hipérbole e é o coeficiente angular dessa reta.
Então as duas equações das assíntotas com serão:
Dessa forma, temos o seguinte gráfico:
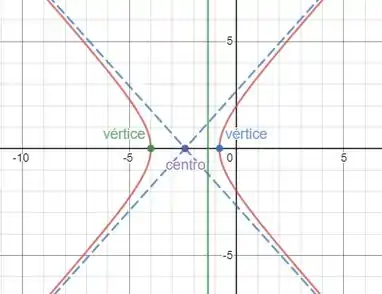
Resposta
a)
b)
c)
d)
