Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.3 - Ex. 12

12 - Encontre a família de soluções de determinada equação diferencial e a família de trajetórias ortogonais. Esboce as duas famílias.

  1. x   d x   +   y   d y   =   0
  2. x   d y   -   2 y   d x   =   0

Passo 1

Resolvendo o item A:

∫ x   d x +   ∫ y   d y = 0

x 2 2 + y 2 2 = C

x 2 + y 2 = C

Realizando a derivação:

2 x + 2 y y ' = 0

2 y y ' = - 2 x

y ' = - 2 x 2 y

y ' = - x y

Para a ortogonal teremos:

d y d x = y x ⇒ d y y = d x x

Resolvendo a Integral:

∫ d y y = ∫ d x x

ln ⁡ y = ln ⁡ x + C

Assim:

y = C x   p a r a   C = e c

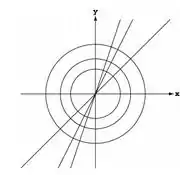
Passo 2

Resolvendo o item B:

x   d y   -   2 y   d x   =   0 ⇒ x   d y = 2 y   d x

Desta forma:

d y 2 y = d x x

∫ d y 2 y = ∫ d x x

1 2 ln ⁡ y = ln ⁡ x + C

y = C 1 x 2 – Equação da família.

Agora:

1 2 ln ⁡ y - ln ⁡ x = C

1 2 y ' y - 1 x = 0

y ' 2 y = 1 x

y ' = 2 y x

Para a ortogonal teremos:

d y d x = - x 2 y

2 y   d y =   - x   d x

∫ 2 y   d y = ∫ - x   d x

y 2 = - x 2 2 + C

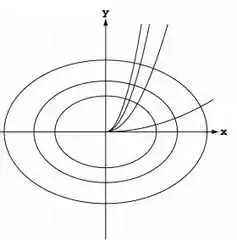
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Percurso de um encouraçado Suponha que um encouraçado de classe Iowa tenha massa em torno de 51.000 toneladas métricas (51.000.000 kg) e um valor k na Equação 1 de cerca de 59.000 kg/s. Suponha que o
Percurso de uma bicicleta Um ciclista de 66 kg em uma bicicleta de 7 kg inicia seu percurso no nível do solo a 9 m/s. O k na Equação 1 é de cerca de 3,9 kg/s.a- Que distância o ciclista irá percorrer
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.9 - y = c e - x
11 - Mostre que as curvas 2 x 2 + 3 y 2 = 5 e y 2 = x 3 são ortogonais.
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.10 - y = e k x