Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.3 - Ex. 11

11 - Mostre que as curvas 2 x^2 + 3 y^2 = 5 e y^2 = x^3 são ortogonais.

Passo 1

Vamos plotar as curvas:

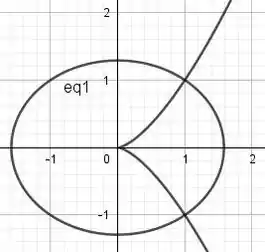
Podemos observar que a intersecção das retas se dão no ponto: ( 1,1 ) .

Passo 2

Assim:

2 x^2 + 3 y^2 = 5 => 4 x + 6 y y^' = 0

6 y y^' = - 4 x => y^' = - (4 x)/(6 y) -> - (2 x)/(3 y)

E

y^' (1,1) = - (2 * 1)/(3 * 1) = - (2)/(3)

Passo 3

Deste modo:

y_1^2 = x^3 => 2 y_1 y_1^' = 3 x^2

y_1^' = (3 x^2)/(2 y)

E

y_1^' (1,1) = (3 * 1^2)/(2 * 1) = (3)/(2)

Logo:

y^'_1 * y^' = (3)/(2) * - (2)/(3) = - (6)/(6) = - 1

Logo podemos afirmar que as curvas são ortogonais.

Resposta

São ortogonais!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

y 2 = k x 3 Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
y = k x Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.8 - 2 x 2 + y 2 = c 2
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.6 - y = c x 2
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.6 - k x 2 + y 2 = 1