Se o fazendeiro no Exercício quiser englobar metros quadrados de terra, que dimensões minimizarão o custo da cerca?
Passo 1
Oi, galera! Tudo bem? 😊
Para fazermos essa questão, precisamos de algumas informações do exercício que não estão no enunciado desse exercício. Para facilitar o nosso trabalho, vou colocar elas aqui, beleza?
- Um fazendeiro quer construir uma cerca em um lote retangular de terra.
- O Fazendeiro não vai construir cerca na parede adjacente ao seu celeiro.
- Na parede compartilhada com o vizinho, os custos para a instalação da cerca serão divididos.
- A instalação da cerca custa por metro linear.
A figura abaixo é uma representação da área que deve ser cercada.
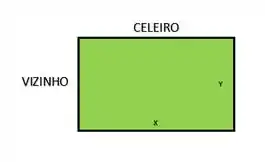
Agora que temos mais informações, conseguimos entender um pouco melhor o que a questão quer. Precisamos encontrar quais valores de comprimento e largura que a região deve possuir, de forma que a sua área total seja de de terra e o custo de instalação da cerca seja o menor possível.
Lembrando que a área de um retângulo é dada através dos valores de comprimento e largura da seguinte forma:
Vamos resolver essa questão por partes, combinado? Faremos o seguinte:
- Encontrar uma função de custo para a instalação da cerca
- Derivar essa função para encontrar os seus pontos críticos, ou seja, resolver a equação
- Verificar se o ponto crítico encontrado é realmente um ponto de mínimo.
- Encontrar o comprimento e a largura que delimitam uma uma região com de tal forma que o custo de instalação da cerca seja mínimo.
Bora colocar a mão na massa?😊
Passo 2
A partir das informações do Passo 1, conseguimos expressar a função que representa o custo que o fazendeiro terá com a instalação da cerca.
Bem, pensa aqui comigo: O custo de instalação da cerca é por metro linear e estamos assumindo que a parede compartilhada com o vizinho é um dos lados de medida .
Dessa forma:
- Como a parede adjacente ao celeiro não terá cerca, então será o custo para cercar um lado do terreno de medida .
- Como a instalação na parede adjacente ao vizinho terá seu custo dividido, então 1 será o custo para cercar o lado compartilhado com o vizinho e será o custo para o outro lado de medida .
Assim, o custo total para cercar o terreno será dado por:
ou seja,
Para tornar as coisas mais fáceis, podemos deixar essa função em termos de apenas uma variável. Pela fórmula da área, temos uma relação entre comprimento e largura. Como
então
e podemos reescrever a função custo da seguinte forma:
Simplificando temos
Pronto, agora que já temos uma expressão para a função custo, vamos encontrar seus pontos críticos nos próximos passos.
Passo 3
Para minimizar a função
vamos começar encontrando os seus pontos críticos a partir da sua derivada.
A função é um polinômio, então vamos derivá-la utilizando a Regra da Soma e, para cada um dos seus termos, vamos utilizar Regra da Potência.
Relembrando a Regra da Potência:
Assim,
Derivando cada um dos termos:
Pronto, encontramos a derivada da função custo. Agora vamos encontrar o seu ponto crítico.
Fazendo vamos ter:
ou seja,
Tomando a raiz quadrada de , vamos ter que o ponto crítico é dado por
Note que também é um ponto crítico da função , mas um valor negativo para o comprimento do retângulo não possui significado físico no problema em questão.
Passo 4
Para checarmos se esse é um ponto de mínimo da função, encontramos a segunda derivada da função (usando as Regras da Soma e da Potência de novo):
e verificamos se ela é positiva no ponto crítico .
Oras, como
pois ambos os termos da fração são positivos, então é um ponto de mínimo.
Passo 5
Para finalizar, precisamos encontrar o comprimento e a largura do terreno com área de e com menor custo de instalação de cerca.
Lembrando que vimos no Passo 2 que
então substituindo o comprimento mínimo encontrado,
é a largura mínima procurada.
Podemos aproximar os valores de e tomando
Assim,
Resposta
Para que o fazendeiro consiga englobar metros quadrados de terra de forma que o custo de instalação da cerca seja mínimo, as dimensões do terreno devem ser de: