Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 5
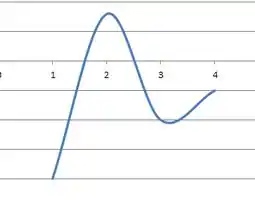
1-3.Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de .
1.(a)
)
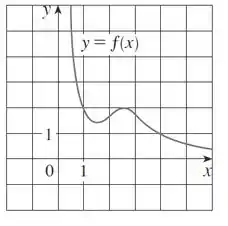
Passo 1
Não esqueça que a derivada de uma curva num ponto é a tangente da curva no ponto considerado. Essa propriedade que iremos usar para resolvermos nosso problema. E caso a reta tenha inclinação negativa a sua tangente será negativa!! Sem mais enrolação, vamos começar.
Passo 2
Começaremos por , traçaremos a tangente e usaremos os quadradinhos como referência para achar a tangente!
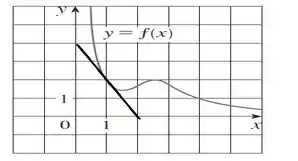
é negativo, pois a inclinação é negativa:
Agora faremos o :
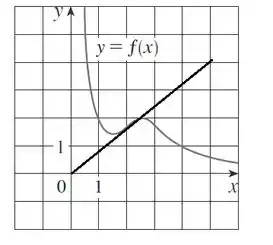
é positivo, pois a inclinação é postiva:
Estamos na , não perca a conta.
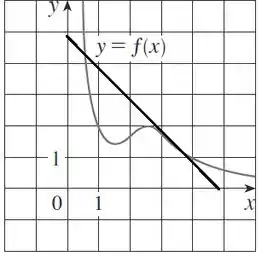
Não ficou certinho no quadrado, porém, a questão pede para estimarmos, então a gente pode dar uma aproximada! Finge que formou quadrados certinhos!
é negativo, pois a inclinação é negativa:
Passo 3
Para não deixarmos o passo muito grande, faremos o e o gráfico da derivada nesse passo.
é negativo, pois a inclinação é negativa:
Reunindo todos os pontos, temos que para o gráfico da derivada:
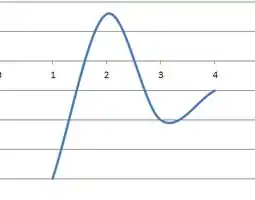
Resposta
