Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 11

11. Seja f ( x ) = 3 x . Estime o valor de f ´ ( 1 ) de duas maneiras:

(a) Use a Definição 2 e tome os valores sucessivamente menores de h .

(b) Dê um zoom sobre o gráfico de y = 3 x e estime a sua inclinação

Passo 1

A definição 2 diz o seguinte pra gente:

f ' ( a ) = lim h → 0 ⁡ f ( a + h ) - f ( a ) h

Passo 2

Com a definição escrita no passo anterior, vamos trocar o valor de a por 1 .

f ' ( 1 ) = lim h → 0 ⁡ f ( 1 + h ) - f ( 1 ) h

f ( 1 + h ) = 3 ( 1 + h )

f ( 1 ) = 3

f ' ( 1 ) = lim h → 0 ⁡ 3 ( 1 + h ) - 3 h

Apenas para facilitar um pouco as nossas contas, botarei o 3 em evidência.

f ' ( 1 ) = lim h → 0 ⁡ 3 ( 3 h - 1 ) h

Vamos construir a tabela jogando os valores próximos de h .

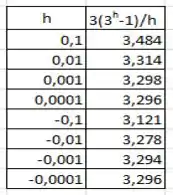
A média de todos esses valores é 3,298 . Logo estimamos o valor de

f ' ( 1 ) = lim h → 0 ⁡ 3 ( 3 h - 1 ) h = 3,298

Passo 3

Agora, faremos a estimativa por meio do gráfico!

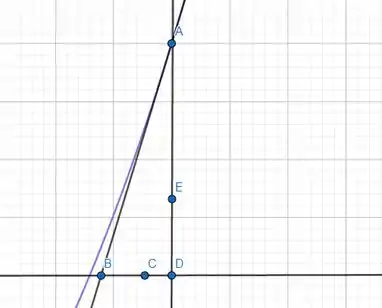
A nossa escala será que o quadrado grande tem 1 cm de lado.

O comprimento de A D é de 4 cm

O comprimento de BD será aproximadamente de 1,2cm.

f ' ( 1 ) = t g ( B D A ) = A D B D = 4 1,2 = 3,33

Resposta

(a)

f ' ( 1 ) = 3,298

(b)

f ' ( 1 ) = 3,33

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quantas retas tangentes à curva y = x / ( x + 1 ) passam pelo ponto ( 1 ,2 ) ? Em quais pontos essas retas tangentes tocam a curva?