Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 35

35. (a) Use o método de Newton para encontrar os números críticos da função f x = x 6 - x 4 + 3 x 3 - 2 x com precisão de três casas decimais. (b) Encontre o valor mínimo absoluto de f com precisão de quatro casas decimais.

Passo 1

Oie, tudo bem? Quero te ajudar a resolver essa atividade.

Aqui a gente primeiro quer encontrar os números críticos da função f x . A gente quer fazer isso utilizando o método de Newton.

Nossa função é a seguinte:

f x = x 6 - x 4 + 3 x 3 - 2 x

Como queremos achar os pontos críticos vamos derivar e igualar a zero. Assim,

6 x 5 - 4 x 3 + 9 x 2 - 2 = 0

Vamos lá aplicar o método de Newton para encontrar as raízes dessa derivada, para isso vamos usar sua fórmula:

x n = x n - 1 - f x n f ' x n

O método consiste em aplicar a fórmula em ciclos até obtermos dois resultados iguais com a precisão desejada.

Veja que teremos também que derivar a derivada, e veja que teremos que encontrar um x n - 1 inicial, a gente costuma procurar um x n - 1 inicial no esboço do gráfico.

Aqui a gente vai utilizar o geogebra para gerar o gráfico.

Fazendo um gráfico, temos:

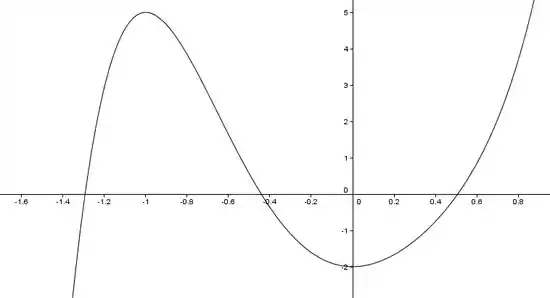
Para a letra b) vamos checar os resultados que obtivemos na letra a) ver qual dos pontos críticos é um mínimo absoluto.

Passo 2

  1. Agora é só usar aquela formula da teoria:

    x n = x n - 1 - f x n - 1 f ' x n - 1

    Lá do Passo 1 a gente fez a derivada de f :

    g x = 6 x 5 - 4 x 3 + 9 x 2 - 2

    Derivando novamente como já tínhamos comentado:

    g ' x = 30 x 4 - 12 x 2 + 18 x

    Arrumando as coisas, temos:

    x n = x n - 1 - 6 x n - 1 5 - 4 x n - 1 3 + 9 x n - 1 2 - 2 30 x n - 1 4 - 12 x n - 1 2 + 18 x n - 1

    Olhando o gráfico, podemos ver que é interessante pegar os pontos:

    x 1 = - 1,3 ;   x 1 = - 0,4   ;   x 1 = 0,5

    Para serem nossos x n - 1

    Passo 3

    Para o ponto x 1 = - 1,3 :

    x n = x n - 1 - 6 x n - 1 5 - 4 x n - 1 3 + 9 x n - 1 2 - 2 30 x n - 1 4 - 12 x n - 1 2 + 18 x n - 1

    Fazendo as contas:

    x 2 = x 1 - 6 x 1 5 - 4 x 1 3 + 9 x 1 2 - 2 30 x 1 4 - 12 x 1 2 + 18 x 1

    x 2 ≈ - 1,29334381

    Para x 3 :

    x 3 = x 2 - 6 x 2 5 - 4 x 2 3 + 9 x 2 2 - 2 30 x 2 4 - 12 x 2 2 + 18 x 2

    x 3 ≈ - 1,29322748

    Para x 4 :

    x 4 = x 3 - 6 x 3 5 - 4 x 3 3 + 9 x 3 2 - 2 30 x 3 4 - 12 x 3 2 + 18 x 3

    x 4 ≈ - 1,29322744

    Para x 5 :

    x 5 = x 4 - 6 x 4 5 - 4 x 4 3 + 9 x 4 2 - 2 30 x 4 4 - 12 x 4 2 + 18 x 4

    x 5 ≈ - 1,29322744

    Opa, como deu igual já podemos parar. Pois nos aproximamos o suficiente da raiz. Logo, a raiz aproximada de oito casas decimais será

    - 1,29322744

    Passo 4

    Para outra raiz, vamos pegar x 1 = - 0,4 . A gente repete todooo aquele processo que já fizemos, agora com outro valor x 1 :

    Para x 2 :

    x 2 ≈ - 0,44375479

    Para x 3 :

    x 3 ≈ - 0,44173524

    Para x 4 :

    x 4 ≈ - 0,44173119

    Para x 5 :

    x 5 ≈ - 0,44173119

    Como x 4 ≈ x 5 , nossa raiz será

    - 0,44173119

    Para última raiz, vamos tomar x 1 = 0,5 :

    Para x 2 :

    x 2 ≈ 0,50793651

    Para x 3 :

    x 3 ≈ 0,50785359

    Para x 4 :

    x 4 ≈ 0,50785359

    Como x 3 ≈ x 4 , nossa raiz será

    0,50785359

    Passo 5

Para acharmos o mínimo absoluto, basta verificarmos quais dos pontos críticos possui menor valor para f ( x ) . Assim,

f x = x 6 - x 4 + 3 x 3 - 2 x

Então,

f - 1,29322744 = - 2,0212  

f - 0,44173119 = 0,5942

f 0,50785359 = - 0,6721

Portanto, o mínimo absoluto será

- 2,0212

Resposta

  1. As raízes aproximadas de oito casas decimais são - 1,29322744 ,   - 0,44173119   e 0,50785359 .
  2. - 2,0212
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico.y = sqrt(x^2 - 4)
Esboce o gráfico.g (x) = x e^(- 3 x)
Esboce o gráfico.f (x) = 2 x + 1 + e^(- x)
Esboce o gráfico.y = (x^3 - x + 1)/(x^2)
Esboce o gráfico.y = (x^2)/(x + 1)