Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 37
37. (a) Use o método de Newton para encontrar as coordenadas do ponto de inflexão da curva , , com precisão de seis casa decimais.
Passo 1
Fala aí, eu sou o Rafha do Responde Aí e vou te ajudar em mais uma questão!
Aqui temos a seguinte equação:
Com variando de
E queremos encontrar as coordenadas do ponto de inflexão.
Bom, uma curva possui ponto de inflexão quando sua segunda derivada é igual a zero, logo queremos o seguinte:
Isso é, queremos encontrar a raiz da segunda derivada da nossa função .
Para isso vamos usar o método de Newton.
Basicamente, nós começamos com um chute inicial para essa raiz.
E para encontrar o próximo valor, faremos a seguinte iteração:
No nosso caso, nós queremos encontrar não é a raiz da função , mas sim a raiz da sua segunda derivada , portanto, o nosso processo iterativo vai ser na verdade o seguinte:
O enunciado pede para encontrarmos com uma precisão de seis casas decimais, dessa forma, teremos que ir realizando iterações até que o valor encontrado não se altere até a sexta casa decimal.Dá trabalho? Dá... mas a vida é um morango mesmo!
Passo 2
Nossa curva é a seguinte:
Como queremos achar os pontos de inflexão, vamos derivar duas vezes e igualar a zero. Logo,
Derivando, usando a regra do produto:
Derivando novamente:
E aqui queremos encontrar a raiz dessa segunda derivada (que é o ponto de inflexão da curva, logo):
Para não confundir, vamos chamar essa segunda derivada de uma nova função .
Agora é só usar aquela formula da teoria:
Ainda precisamos da derivada dessa função, logo, derivando novamente, teremos:
Passo 3
Agora sim, podemos usar a fórmula:
Para a primeira iteração, precisamos de um chute inicial. Como o domínio para é
Vamos usar como chute inicial, o valor intermediário do domínio, isso é:
Fazendo as contas:
Para :
Para :
Para
Opa, como deu igual já podemos parar. Pois nos aproximamos o suficiente da raiz. Logo, a raiz aproximada de seis casas decimais será .
Lembrando que esse é o valor onde
E a nada mais é que a segunda derivada da nossa função .
Logo, encontramos o valor do ponto de inflexão da nossa função .
Passo 4
Para finalizar, vamos encontrar o valor da no ponto que encontramos.
Nossa função é
Usando o ponto dado, temos:
A questão acaba aqui!
Mas por motivos didáticos, eu vou apenas plotar o gráfico da função para mostrar para vocês que de fato encontramos uma coordenada que faça sentido, isso é, a coordenada do ponto de inflexão desse gráfico.
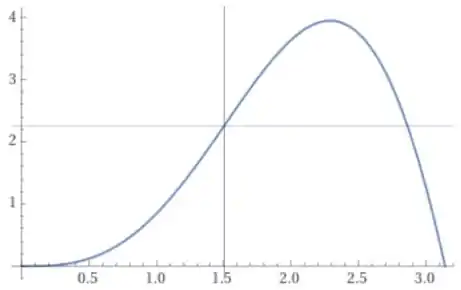
De fato, a coordenada que encontramos é um ponto onde o gráfico de deixa de ter concavidade para cima e passa a ter concavidade para baixo, ou seja, é um ponto de inflexão.