Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.1 - Ex. 14

14. Complete os cálculos que levam aos elementos nas colunas três e quatro da tabela 8.1 . 2

Passo 1

Bora lá pro nosso probleminha!

Olha só! A fórmula de E u l e r   i n v e r s a   para a equação diferencial desse probleminha tem a seguinte cara...

y n + 1 = y n + h ( 1 - t n + 1 + 4 y n + 1 )

Isolando y n + 1 , ficamos com...

y n + 1 = y n + h - h t n + 1 1 - 4 h

Onde sabemos que...

y 0 = 1

De modo que sabendo que h = 0,01 ... Para chegarmos até um valor de t   igual a 2 , será preciso um total de iterações igual à...

T o t a l   d e   i t e r a ç õ e s = 2 0,01 = 200

Passo 2

E conforme pede o problema, vamos utilizar um método computacional simples... Um códigozinho simples em C , C + + ou P y t h o n resolveria isso.

Para isso, basta usar a seguinte estrututa na confecção do código...

P a s s o   1 : D e f i n i r   a   f u n ç ã o   y n + 1   e m   f u n ç ã o   d e   y n , h   e   t n + 1 .

P a s s o   2 : D e f i n i r   o   t a m a n h o   d o   p a s s o   h   e   o   n ú m e r o   d e   p a s s o s   n

P a s s o   3 : P a r a   i   d e   1   a t é   u m   t a m a n h o   d e 2 h   f a ç a

P a s s o   4 :

y n + 1 = y n + h - h t n + 1 1 - 4 h

i = i + 1

n = n + 1

P a s s o   5 : E s c r e v a l   y n + 1

P a s s o   6 : F i m

É importante trabalhar com y n + 1 e y n na forma de vetor! Facilita muito a nossa vida!

Bom! Usando o seguinte código confeccionado em C ...

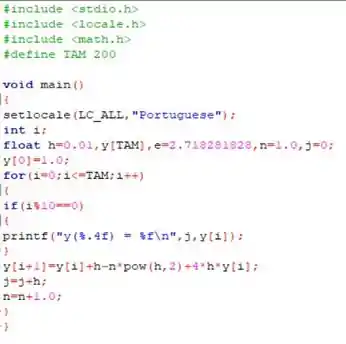
Chegamos até o seguinte resultado...

t = 0 → y 0 = 1,000

t = 0,1 → y 0,1 = 1,6236638

t = 0,2 → y 0,2 = 2,5491368

t = 0,3 → y 0,3 =   3,9285724

t = 0,4 → y 0,4 = 5,9908303  

t = 0,5 → y 0,5 = 9,0801473  

t = 1,0 → y 1,0 =   70,452395  

t = 1,5 → y 1,5 =   542,12432  

t = 2,0 → y 2,0 =   4172,7228  

Passo 3

Já no caso de h valer 0,001 , que é a nossa coluna quatro...

O tamanho de iterações de n vai ser dado por:

T o t a l   d e   i t e r a ç õ e s = 2 0,001 = 2000

De modo que compilando o código, alterando apenas o tamanho de iterações e o valor de h , obtemos que...

t = 0 → y 0 = 1,000

t = 0,1 → y 0,1 = 1,6104634

t = 0,2 → y 0,2 =   2,5095731  

t = 0,3 → y 0,3 =   3,8396379  

t = 0,4 → y 0,4 =   5,8131282    

t = 0,5 → y 0,5 =   8,7472667    

t = 1,0 → y 1,0 = 65,419964  

t = 1,5 → y 1,5 =   485,05825    

t = 2,0 → y 2,0 =   3597,4478  

E pronto! Encerramos por aqui!

Resposta

Para a coluna 3:

t = 0 → y 0 = 1,000

t = 0,1 → y 0,1 = 1,6236638

t = 0,2 → y 0,2 = 2,5491368

t = 0,3 → y 0,3 =   3,9285724

t = 0,4 → y 0,4 = 5,9908303  

t = 0,5 → y 0,5 = 9,0801473  

t = 1,0 → y 1,0 =   70,452395  

t = 1,5 → y 1,5 =   542,12432  

t = 2,0 → y 2,0 =   4172,7228  

Para a coluna 4:

t = 0 → y 0 = 1,000

t = 0,1 → y 0,1 = 1,6104634

t = 0,2 → y 0,2 =   2,5095731  

t = 0,3 → y 0,3 =   3,8396379  

t = 0,4 → y 0,4 =   5,8131282    

t = 0,5 → y 0,5 =   8,7472667    

t = 1,0 → y 1,0 = 65,419964  

t = 1,5 → y 1,5 =   485,05825    

t = 2,0 → y 2,0 =   3597,4478  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de23 a 26,use a fórmula de Euler modificada do Problema 22 com h=0,05 para calcular valores aproximados da solução do problema de valor inicial dado em t=0,1 ;0,2 ;0,3e0,4 . C
Em cada um dos problemas de23 a 26,use a fórmula de Euler modificada do Problema 22 com h=0,05 para calcular valores aproximados da solução do problema de valor inicial dado em t=0,1 ;0,2 ;0,3e0,4 . C
27. Mostre que a fórmula de Euler modificada do Problema 22 será idêntica à fórmula de Euler aprimorada da E q .( 5 ) para y ' =f ( t ,y ) se f for linear em ambos t e y .
Em cada um dos problemas de23 a 26, use a fórmula de Euler modificada do Problem 22 com h=0,05 para calcular valores aproximados da solução do problema de valor inicial dado em t=0,1 ;0,2 ;0,3e0,4 . C
14. Nesse problema, vamos provar que o erro de truncamento local para a fórmula de E u l e r aprimorada é proporcional a h 3 . Se supusermos que a solução ϕ do problema de valor inicial y ' = f t , y