Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 3

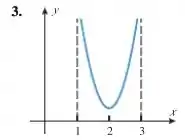
1-4. Seja a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes é contínua?

3.

a)

b)

c)

d)

e)

f)

Passo 1

Então pessoal, antes de respondermos as questões, devemos lembrar de um pequeno detalhe, que é a notação de e em intervalos! Quando há parênteses, isso implica que o intervalo é aberto, ou seja, a função não precisa estar definida exatamente no valor do intervalo, ok? Por outro lado, quando há colchetes, isso implica que o intervalo é fechado e a função está definida exatamente no valor do intervalo!

Outra coisa que vale ressaltar é que o limite não existe se os limites laterais não existirem, beleza? Sabendo disso já podemos responder as questões, então bora lá!

a) Então galera, aqui temos um intervalo fechado de a , ou seja, o intervalo está dizendo que a função é definida em e definida em também, mas isso não é o que vemos no gráfico! No gráfico a função não está definida nesses dois valores, então podemos dizer que o intervalo não é contínuo.

b) Diferentemente da letra a), como aqui o intervalo está aberto, não importa se a função está ou não definida em e em , então podemos dizer que o intervalo é contínuo nesse caso.

Passo 2

c) Pelo mesmo motivo da letra a), a função não está definida em e o intervalo diz que a função está. Dessa forma, podemos dizer que o intervalo não é contínuo.

d) O intervalo que nos foi dado é aberto, ou seja, não nos importa se a função está ou não definida em e , nos importa apenas se ela está definida nas proximidades destes pontos. Observando o gráfico conseguimos notar que, de fato, em a função não está definida, mas está definida em todos os outros pontos até , então podemos dizer que o intervalo é contínuo.

Passo 3

e) Pelo mesmo motivo da letra a), a função não está definida em e o intervalo diz que a função está. Dessa forma, podemos dizer que o intervalo não é contínuo.

f) O intervalo que nos foi dado é aberto, ou seja, não nos importa se a função está ou não definida em e , nos importa apenas se ela está definida nas proximidades destes pontos. Observando o gráfico conseguimos notar que, de fato, em a função não está definida, mas está definida em todos os outros pontos anteriores até , então podemos dizer que o intervalo é contínuo.