Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.6 - Ex. 47
14.47. Se , determine o vetor gradiente e use-o para determinar a reta tangente à curva de nível da função no ponto . Esboce as curvas de nível, reta tangente e vetor gradiente.
Passo 1
O operador gradiente é um vetor contido no domínio de uma função. Ele é perpendicular às curvas de nível, tendo direção e sentido apontando para onde há maior variação. Sua definição é dada por
Para calculá-lo, portanto, é necessário calcular as derivadas parciais da função em um ponto arbitrário e depois substituir esse ponto pelo pedido na questão, a saber .
Para obter a reta tangente à curva de nível é necessário encontrar um vetor tal que
Essa equação mostra que o vetor encontrado deverá ser perpendicular ao vetor gradiente. Dito isso, o vetor encontrado será tangente à curva de nível.
Obtidos todos os resultados será esboçado um gráfico contendo as curvas de nível.
Passo 2
O primeiro passo será calcular as derivadas parciais para se obter o vetor gradiente. Começando com a derivada em
Calculando a derivada em
Com isso obtemos o vetor gradiente
Passo 3
Substituindo no vetor gradiente o ponto solicitado pela questão, temos
Passo 4
Para calcular o vetor tangente, basta resolver a equação
Em que e são variáveis a serem encontradas. Essas variáveis representam os coeficientes que nos dão a direção e sentido do vetor tangente. Como é um vetor que tem como sua origem o ponto , os valores dessas variáveis devem ser
Substituindo esse resultado na primeira equação apresentada neste passo, podemos resolver o produto escalar
Com isso, obtemos uma equação para a reta tangente à curva de nível no ponto
Passo 5
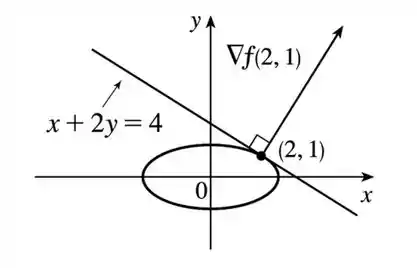
Obtidos todos os valores solicitados, podemos montar um gráfico.
Primeiro precisamos encontrar qual é a expressão gráfica da curva de nível, e para isso basta substituir na função
Essa é a equação de uma elipse no plano que será esboçada em nosso gráfico.
Para esboçar o vetor gradiente, basta encontrar no gráfico o ponto e desenhar nele um vetor seguindo a expressão
A reta tangente é esboçada de acordo com a sua equação
Resposta
𝐴 equação da reta é
O vetor gradiente é dado por
O desenho do gráfico foi demonstrado.