Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 15-a

15 . Suponha que determinada população satisfaz o problema de valor inicial

dy/dt = r(t)y – k,

y(0) = y0,

em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predatória.(a) Suponha que k = 1/5. Faça gráficos de y em função de t para diversos valores de y0 entre ½e 1.(b) Estime a população inicial crítica yc abaixo da qual a população será extinta.(c) Escolha outros valores de k e encontre a população crítica yc correspondente para cada umdeles.(d) Use os dados encontrados nos itens (b) e (c) para fazer o gráfico de yc em função de k.

Passo 1

Bem galera, antes de fazermos os gráficos e todas as análises que o exercício, precisamos resolver essa equação diferencial. Tenho que admitir que essa não é uma equação tão trivial assim. Afinal ela não é separável. Temos que usar o método de Termo Integrante para solucionar! Ele é bem simples e consiste em deixar nossa função com a seguinte cara

y ' + p t y = q t

Onde a solução tem o seguinte formato

y = 1 I t ∫ I t   q t d t + C

Onde nossa função I t   é

I t = e ∫ P t d t

Belezinha? Vamos cair dentro então \o/

Passo 2

Então nossa equação é

d y d t   =   r ( t ) y   –   k ,  

Vamos manipular ela um pouquinho para ficar mais evidente o que precisamos fazer

y ' - r y = - k

Agora é só aplicar a formulinha. Vamos primeiro encontrar o termo integrante

I t = e ∫ P t d t

I t = e ∫ - r d t

I t = e - ∫ 1   + sen ⁡ t 5 d t

I t = e - t 5 + cos ⁡ t 5

Passo 3

Agora vamos descobrir como é a nossa solução

y = 1 I t ∫ I t   q t d t + C

y = 1 e - t 5 + cos ⁡ t 5 ∫ e - t 5 + cos ⁡ t 5   k d t + C

y = 1 e - t 5 + cos ⁡ t 5 ∫ e - t 5 + cos ⁡ t 5   - 1 5 d t + C

E infelizmente a integral ∫ e - t 5 + cos ⁡ t 5   - 1 5 d t não tem solução analítica, apenas numérica. Mas , Podemos fazer umas manipulações para achar C. Sabendo que

y 0 = y 0

y = 1 e - t 5 + cos ⁡ t 5 ∫ e - t 5 + cos ⁡ t 5   - 1 5 d t + C

y 0 = 1 e 1 5 ∫ e - t 5 + cos ⁡ t 5   - 1 5 d t + C

C = y 0 e 1 5 + 1 5 ∫ e - t 5 + cos ⁡ t 5   d t

Só para nossa equação ficar mais bonita podemos fizer o seguinte a solução dessa integral pode dessa encontrada por meio de uma expansão em serie de Taylor, e podemos observar ela abaixo

Vemos que todos os termos dessa expansão dependem de t, logo se t → 0 essa função tende a zero também. Logo podemos dizer que

C = y 0 e 1 5

E por fim nossa equação fica com a seguinte resposta

y = 1 e - t 5 + cos ⁡ t 5 ∫ e - t 5 + cos ⁡ t 5   - 1 5 d t + y 0 e 1 5

Podemos manipular um pouco essa equação ficar um pouco mais palatável

y = 1 e cos ⁡ t - t - 1 5 ∫ e cos ⁡ t - t   d t + y 0

Passo 4

Vamos construir gráficos para y com diversos valores de y 0 , como fazer o gráfico de uma integral é complicado, então vamos plotar o gráfico da expansão de Taylor dessa integral

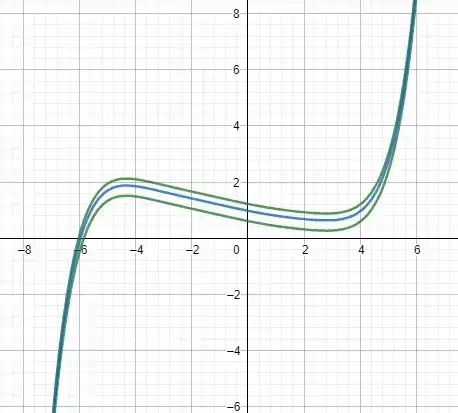
AS curvas são referentes a y 0 = 1 2   , 4 5   ,   1 . Podemos Observar que a relevância do y 0 se vale apenas para o inicio da função, e logo o comportamento se torna igual para todas as curvas de nível.

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

y = 1 e cos ⁡ t - t - 1 5 ∫ e cos ⁡ t - t   d t + y 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando um procedimento semelhante ao que abordamos no texto sobre o modelo de caçador competitivo, mostre que, à medida que o tempo t aumenta, cada trajetória é percorrida em sentido anti-horário. Ao
Mostre, por meio de diferenciação, que a função C t = a ⋅ ln ⁡ y t - b ⋅ y t - d ⋅ x t + c ⋅ ln ⁡ x t é constante quando x ( t ) e y ( t ) são positivos e satisfazem as equações presa-predador. Enquan
Aproximação do equilíbrio por duas trajetórias. Mostre que as duas trajetórias que conduzem a ( m / n ,a / b ) mostradas na Figura 9.31 são únicas por meio dos passos seguintes.A partir do sistema 1 a
Difusão de informação. Os sociólogos reconhecem um fenômeno chamado difusão social, que é a propagação de uma informação, inovação tecnológica ou modismo cultural entre a população. Os membros da popu
As equações diferenciais autônomas representam modelos de crescimento populacional. Use a análise da reta de fase para esboçar curvas integrais P ( t ) , selecionando diferentes valores iniciais P ( 0