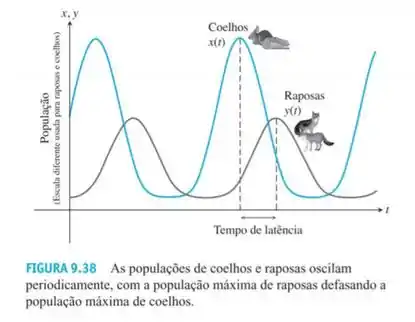
Usando um procedimento semelhante ao que abordamos no texto sobre o modelo de caçador competitivo, mostre que, à medida que o tempo aumenta, cada trajetória é percorrida em sentido anti-horário. Ao longo de cada trajetória, tanto as populações de coelhos como as de raposas flutuam entre seus níveis máximos e mínimos. Os níveis máximo e mínimo da população de coelhos surgem onde a trajetória intercepta a reta horizontal . No caso da população de raposas, manifestam-se onde a trajetória intercepta a reta vertical . Quando a população de coelhos estiver em seu máximo, a população de raposas estará abaixo de seu valor máximo. À medida que a população de coelhos diminui nesse instante no tempo, passamos a nos mover no sentido anti-horário em torno da trajetória, e a população de raposas cresce até atingir seu valor máximo. Nesse ponto, a população de coelhos terá diminuído para e não estará mais em seu valor de pico. Vemos que a população de raposas atinge seu valor máximo em um instante posterior ao dos coelhos. A população do predador fica para trás para atingir seus valores máximos. Esse efeito de latência é mostrado na Figura 9.38, que representa graficamente tanto como

Vamos considerar uma trajetória específica e supor tal que e , então, e isso implica que a população de coelhos está aumentando enquanto a população de raposas está diminuindo, ou seja, os pontos na trajetória estão se movendo para baixo e para direita. Agora, se e , então, e isso vai implicar que tanto as populações de coelhos como a de raposas estarão aumentando, ou seja, os pontos na trajetória estão subindo e à direita.

Podemos considerar também se e , então, e , assim, a população de coelhos está diminuindo enquanto a população de raposas está crescendo, os pontos na trajetória, então, estão subindo e a esquerda. Por fim, se e , então, e isso indica que tanto a população de coelhos como a população de raposas estão diminuindo, os pontos na trajetória estão se movendo para baixo e para a esquerda.

Dessa forma, os pontos percorrem a trajetória no sentido – horário, observe, ainda, que seguiremos a mesma trajetória começar em um ponto diferente da trajetória.