Aproximação do equilíbrio por duas trajetórias. Mostre que as duas trajetórias que conduzem a mostradas na Figura 9.31 são únicas por meio dos passos seguintes.

1. A partir do sistema e , aplique a regra da cadeia para deduzir a seguinte equação:
2. Separe as variáveis, integre e calcule a exponencial para obter

K é uma constante de integração.

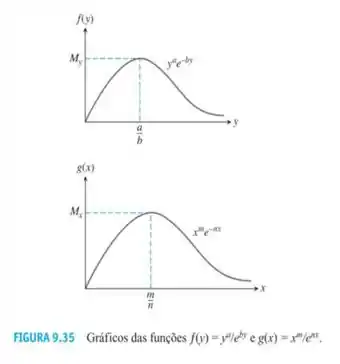
3. Seja e . Mostre que tem um único máximo quando , como mostra a Figura 9.35. Do mesmo modo, mostre que tem um único máximo quando, também mostrado na Figura 9.35.



4. Considere o que acontece quando se aproxima de Torne os limites no item (b) quando e para mostrar que

Ou que Assim, qualquer trajetória de solução que se aproxime de deve satisfazer

5. Mostre que apenas uma trajetória pode aproximar por baixo da reta y = a/b. Pegue . A partir da Figura 9.35, podemos verificar que , o que implica em

Isso, por sua vez, implica em

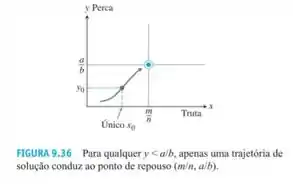
A Figura 9.35 mostra que para existe um único valor que satisfaz essa última desigualdade. Isto é, para cada , existe um único valor de que satisfaz a equação do item (d). Assim, pode existir apenas uma solução de trajetória que aproxima por baixo, como mostra a Figura 9.36.

6. Use um argumento semelhante para mostrar que a trajetória da solução que leva a é única se

Para resolvermos o item A precisamos, primeiramente, saber o que é esse sistema de e que é descrito no texto e representado por

Dando um reformulado nessas equações chegamos em

Precisamos, agora, encontrar e podemos fazer

Seguindo com as sugestões do problema vamos separar as variáveis

Integrando ambos os lados vamos ter

Fazendo

Seguindo a resolução com as dicas dadas no exercício vamos tomar e e buscar seus pontos de máximo e aplicar esses valores na nossa função

Se derivarmos a função mais uma vez e aplicando o ponto

Aplicando esse ponto na nossa equação vamos ter

Fazendo o mesmo procedimento para obteremos

Aplicando esse ponto na nossa função inicial vamos obter

Considerando a trajetória . Tomando, agora, o resultado do item B temos

Aplicando o limite em ambos os lados teremos

Portanto

Representa a equação que qualquer trajetória de soluções deve satisfazer se a trajetória se aproximar do ponto de repouso assintoticamente.

Tomando a condição inicial Então pela figura temos que implica em e, portanto, da figura para presente no item C temos que existe um único que satisfaça da mesma forma para , dessa forma existe apenas uma única trajetória que aproxima por baixo.

Da mesma forma como mostrado anteriormente, existe uma trejetória única quando Novamente, implica e, portanto, . Analisando novamente a figura de mostrada no item C, vemos que existe um único que satisfaz . Ou seja, para cada temos um único que satisfaz . Portanto, só pode existir uma única trajetória se aproximando de .