Difusão de informação. Os sociólogos reconhecem um fenômeno chamado difusão social, que é a propagação de uma informação, inovação tecnológica ou modismo cultural entre a população. Os membros da população podem ser divididos em duas classes: aqueles que têm a informação e aqueles que não a têm. Em uma população fixa com tamanho conhecido, é razoável supor que a taxa de difusão seja proporcional ao número dos que têm a informação vezes o número dos que ainda não a receberam. Se denota a quantidade de indivíduos que têm a informação em uma população de pessoas, então o modelo matemático para a difusão social é dado por
onde representa o tempo em dias e é uma constante positiva.
- Discuta se o modelo é razoável.
- Construa uma reta de fase e identifique os sinais de e .
- Esboce curvas integrais representativas.
- Preveja o valor de com o qual a informação será disseminada mais rapidamente. Quantas pessoas, de fato, receberão a informação?
Passo 1
O modelo parece ser razoável porque a taxa de disseminação de uma informação, uma inovação ou uma moda cultural é proporcional ao produto do número de indivíduos que possuem a informação e daqueles que não a possuem , quando é pequeno existem apenas algumas pessoas com informação e isso vai implicar em uma disseminação lenta enquanto que se tivermos e grandes vamos ter uma propagação da informação mais rápida devido a quantidade de pessoas que sabem sobre.
Passo 2
Partindo do modelo dado vamos encontrar os pontos de equilíbrio para que possamos construir a reta de fase. Lembrando que os pontos de equilíbrio são os pontos onde , assim
Sendo um ponto de equilíbrio instável e o ponto ponto de equilíbrio estável.
Calculando a segunda derivada teremos
Os pontos de inflexão são . Assim,
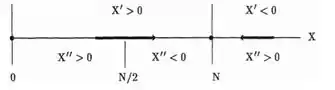
Passo 3
Tomando por base os pontos marcados na reta de fase traçamos assíntotas horinzontais de tal forma a obter curvas integrais de acordo com o comportamento da função dentro do intervalo. Dessa forma, teremos
Passo 4
A informação será disseminada mais rápida quando , ou seja, quando metade da população souber da informação, assim, a informação terá possibilidade de se disseminar mais rapidamente e eventualmente todas as pessoas receberão a notícia.
Resposta
Ei, a resposta está no passo a passo :)