Mostre, por meio de diferenciação, que a função

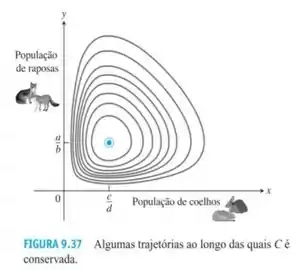
é constante quando e são positivos e satisfazem as equações presa-predador. Enquanto e podem variar com o passar do tempo, não pode. Assim, é uma quantidade conservada, e sua existência fornece uma lei de conservação. Uma trajetória que começa em um ponto no instante fornece um valor de que se mantém inalterado em tempos futuros. Cada valor da constante fornece uma trajetória para o sistema autônomo, e essas trajetórias se fecham, em vez de espiralar para dentro e para fora. As populações de coelho e raposa oscilam através de ciclos repetidos ao longo de uma trajetória fixa. A Figura 9.37 mostra várias trajetórias para o sistema presa-predador.

Vamos pegar nossa função e derivá-la

Para simplificar a visualização vamos fazer as seguintes substituições

Como atende ao sistema de presa-predador podemos substituir e e teremos