Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 17
17. Explique por que a função é descontinua no número dado . Esboce o gráfico da função.
;
Passo 1
Opa, vamos fazer essa questão! O enunciado nos da:
E pede pra a gente explicar porque a função é descontínua em .
Beleza, sabemos que uma função é contínua se:
Tudo que precisamos então é calcular o limite da função quando tende a e ver o que acontece!
Passo 2
Temos então:
Chegamos em uma indeterminação, não podemos ter divisão por zero, agora ficou fácil entender, né! A nossa função é descontínua em porque ela não é definida nesse ponto.
Passo 3
Fazendo um gráfico, temos:
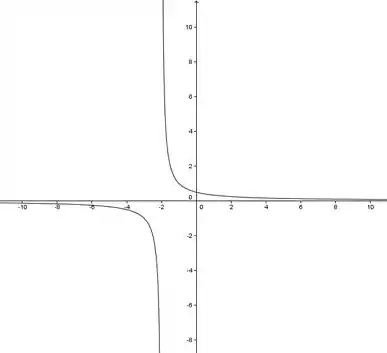
Resposta
- A função é descontínua em porque ela não é definida nesse ponto.
- Esboço do gráfico.
Exercícios de Livros Relacionados
41-42 (a) Complete a tabela e dê uma estimativa para o limite indicado. (b) Encontre o valor exato do limite.41- f x = s e n x - 5 x 2 - 25 ; lim x → 5 f ( x )
49- Encontre um valor diferente de zero para a constante k que torne f ( x ) t g k x x ,x0 3 x + 2 k 2 , x ≥ 0 Contínua em x = 0 .
15-16 Em cada parte, use o Teorema 1.5.6 (b) para mostrar que a função é contínua em toda parte.15- a) s e n ( x 3 + 7 x + 1 ) b) s e n x c) cos 3 ( x + 1 )
9-14 Determine onde f é contínua.10. f x = arccos l n x
50. Será a função f x = s e n x x , x ≠ 0 1 , x = 0 contínua em x = 0 ? Explique.